5. Calcular , onde é a região delimitada por e .
Passo 1
Segue a região de integração.
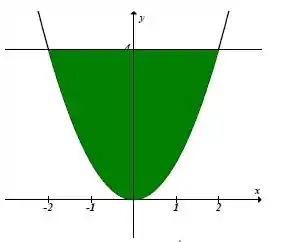
Assim, iremos ter uma região do tipo 1, onde o possui um intervalo numérico.
5. Calcular , onde é a região delimitada por e .
Segue a região de integração.

Assim, iremos ter uma região do tipo 1, onde o possui um intervalo numérico.