Enunciado
Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 12.4 - Ex. 8
Calcule a área do conjunto de todos tais que e .
Passo 1
Como se trata de uma questão extensa, vamos fazê-la por etapas!
Inicialmente, vamos definir:
Vamos isolar na Eq.1:
Dada essa desigualdade, vamos ver o que ela significa geometricamente:
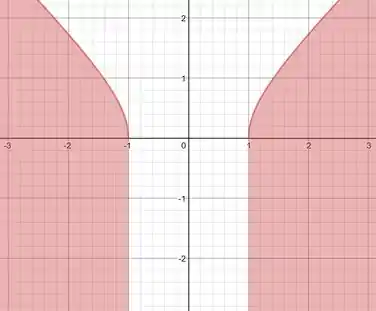
Como é definido que: sabemos que a função é definida para valores positivos de y e a função é definida para valores maiores ou menores de x, para 1 ou -1, como mostrado na figura.
Passo 2
Agora, vamos analisar a Eq.2:
Dada essa desigualdade, vamos ver o que ela significa geometricamente:
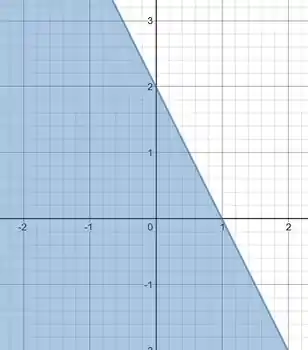
Podemos ver pela figura que nossa função delimita todo o lado esquerdo do gráfico!!
Passo 3
Com isso, vamos calcular a área do gráfico que obedece as duas desigualdades dadas, sobrepondo os gráficos!
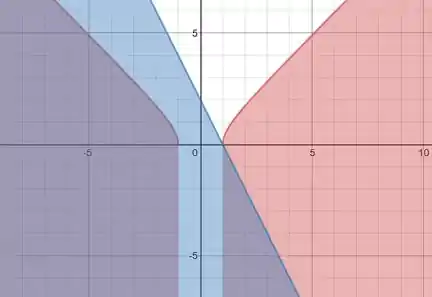
Pelo gráfico, percebemos que nosso intervalo de integração será de -1 até -.
Como a área do gráfico de uma função é dada por uma Integral de Riemman, é necessário lembrar que sempre A>0, logo, a função área dada pelas desigualdades será escrita como:
Passo 4
Resolvendo essa integral, temos que: (Vamos em vez de , usar , para calibrar nossa área em função do x!!