Calcule a área limitada pela curva
E pelo eixo .
Passo 1
Olá, meu amigoooo. Vamos resolver juntos essa atividade.
A gente tem a curva parametrizada:
E a gente quer calcular a área delimitada por essa curva. A, vale lembrar que a nossa curva está delimitada pelo eixo também como diz o enunciado.
A área de uma curva é dada por
Então temos que identificar cada termo dessa integral aí, substituir e calcular.
Antes de iniciarmos, vamos olhar o gráfico gerado pela nossa curva, é uma excelente forma de identificar os intervalos de integração:
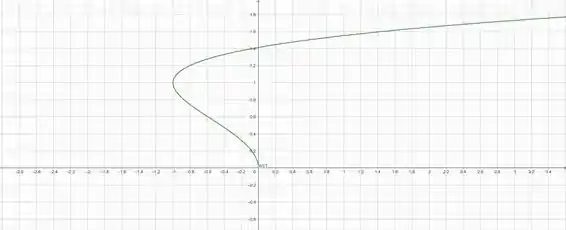
Então a gente ver que a curva toca em em 2 pontos, e são eles que fazem parte do nosso limite de integração.
Passo 2
Para encontrar o intervalo de integração, vamos pensar o seguinte:
Queremos a área entre a curva e o eixo . Só que o eixo é justamente onde o , assim:
Podemos dar uma manipulada:
E encontramos duas soluções:
Ou
Esses são nossos limites de integração!!
Sobre os outros termos da integral, o é a própria parametrização:
Para achar é só pegar a parametrização do e derivar em relação a :
Derivando:
Passo 3
Aí aqui a gente substitui tudo na integral e calcula, vamos relembrar a fórmula geral:
Agora substituindo:
Vamos dar uma organizadinha, abrir esse parênteses pra ficar melhor:
Agora calculando:
Aplicando os limites de integração:
Resolvendo:
Arrumando as raízes:
Agora ficamos com:
Aweeee!