Exercícios de Reta Tangente e Normal a Curva - Lista de Exercícios Resolvida
Questão 2
Considere as duas superfícies dadas por e .
1. Esboce, separadamente, as duas superfícies, mostrando as curvas de interseção com os planos coordenados.
2. Parametrize a curva obtida pela interseção das 2 superfícies.
3. Calcule a reta tangente a no ponto .
4. Existe algum ponto de no qual a reta tangente passe na origem? Justifique.
Ver solução completaQuestão 3
O movimento de uma partícula no intervalo de tempo é descrito pela curva parametrizada .
a) Encontre a equação paramétrica da reta tangente a curva no instante .
b) Suponha que no instante a partícula sai pela tangente em movimento retilíneo uniforme. Ache a posição da partícula no instante .
Ver solução completaQuestão 4
Considere a curva parametrizada por , onde é uma constante. Para que valor de a reta tangente a no ponto passa pelo ponto ?
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 7
Determinar as equações paramétricas da reta tangente à elipse:
no ponto:
Ver solução completaQuestão 8
Seja uma partícula cuja posição no espaço ao longo do tempo é descrita pela função vetorial , com .
Encontre a reta tangente à curva descrita pela partícula no ponto .
Ver solução completaQuestão 9
Sejam e as superfícies
a) Encontre uma parametrização para a curva dada pela interseção de e .
b) Determine a equação da reta tangente à curva do passo anterior, no ponto .
Ver solução completaQuestão 10
Seja a curva dada por . Sabendo que a imagem de está contida na superfície de equação , determine e encontre uma equação para a reta tangente a em
Ver solução completaQuestão 11
O movimento de uma partícula de massa unitária no intervalo de tempo é descrito pela curva parametrizada
- Ache a equação paramétrica (ou vetorial) da reta tangente à curva no instante .
- Suponha que no instante a partícula sai pela tangente em movimento retilíneo uniforme. Ache a distância total percorrida pela partícula do instante até o instante .
Questão 12
Considere a curva , , e o triângulo delimitado pelas retas tangentes a nos pontos . A área deste triângulo é:
Escolha uma opção:
11
33/4
99/2
11/2
99/4
Ver solução completaQuestão 13
Seja o paraboloide elíptico . Determine a equação do plano tangente e a equação paramétrica da reta normal ao paraboloide no ponto
Ver solução completaQuestão 14
Considere a superfície de equação . Seja a curva interseção de com o plano e a reta tangente a no ponto . Marque a opção que identifica a superfície , a curva e dá uma parametrização de , nessa ordem:
- Paraboloide circular, parábola e
- Elipsoide, elipse e
- Elipsoide, elipse e
- Paraboloide circular, circunferência e
- Paraboloide elíptico, elipse e
Questão 15
Considere a curva definida pela função vetorial
onde .
Encontre equações simétricas para a reta tangente à curva no ponto .
Ver solução completaQuestão 16
Qual o ponto da curva , parametrizada por
No qual a reta tangente a contém o ponto ?
Questão 17
A imagem da curva está contida na interseção das superfícies
Se e , a reta tante a em é dada pela equação
Ver solução completa
Questão 18
Seja a curva parametrizada por . Determine os valores de tais que a reta tangente à no ponto intercepta o eixo .
a)
b)
c)
d)
e)
Ver solução completaQuestão 20
Considere as duas superfícies dadas por e .
2. Parametrize a curva obtida pela interseção das 2 superfícies.
3. Calcule a reta tangente a no ponto .
4. Existe algum ponto de no qual a reta tangente passe na origem? Justifique.
Ver solução completaQuestão 21
Considere a superfície dada por
- Enconte uma equação do plano tangente a no ponto .
- Encontre uma equação da reta normal à superfície no ponto .
Questão 22
Considere a curva parametrizada por: . A reta tangente a no ponto corta o eixo no ponto:
a)
b)
c)
d)
e)
f) Nenhuma das alternativas
Ver solução completaQuestão 23
Seja a curva dada pela interseção dos gráficos das funções
- Determine uma parametrização para .
- Determine, caso existam, todos os pontos de nos quais a reta tangente é paralela ao eixo . Escreva a equação da reta tangente em tais pontos.
Questão 25
Considere a curva parametrizada pelas equações e , possui um ponto de auto-inserção que está na reta . Qual é este ponto e quais são as equações das retas tangentes a em tal ponto?
a)
b)
c)
d)
e) Nenhuma das alternativas
Ver solução completaQuestão 26
Considere
Considere a curva plana parametrizada , obtida pela projeção de no plano .
- Encontre uma curva de nível (no plano ) dada por tal que o traço de está contido em . Explicite .
- Escreva o vetor normal a no ponto e exiba a equação cartesiana da reta tangente à em .
Questão 27
(Capítulo 13.2 – Exercício 4)
(a) Esboce o gráfico da curva plana com a equação vetorial dada.
(b) Encontre r’(t)
(c) Esboce o vetor posição r(t) e o vetor tangente r’(t) para o valor dado de t.
Ver solução completaQuestão 28
(Capítulo 13.2 – Exercício 5)
(a) Esboce o gráfico da curva plana com equação vetorial dada.
(b) Determine r’(t).
(c) Esboce o vetor posição r(t) e o vetor tangente r’(t) para o valor dado de t.
Ver solução completaQuestão 29
(Capítulo 13.2 – Exercício 17)
Determine o vetor tangente unitário T(t) no ponto com valor de parâmetro dado t.
Ver solução completaQuestão 30
(Cap. 13.2 - Ex. 29)Determine as equações paramétricas para a reta tangente à curva dada pelas equações paramétricas, no ponto especificado. Ilustre traçando o gráfico da curva e da reta tangente em uma mesma tela.
Ver solução completaQuestão 31
(Cap. 13.2 - Ex. 34) Em que ponto as curvas e se cruzam? Determine o ângulo de intersecção destas, com precisão de um grau.
Ver solução completaQuestão 32
(Cap. 13.2 - Ex. 32) (a) Determine o ponto de intersecção das retas tangentes à curva
nos pontos e .
(b) Ilustre traçando o gráfico da curva e ambas as tangentes.
Ver solução completaQuestão 33
O movimento de uma partícula no intervalo de tempo é descrito pela curva parametrizada .
a) Encontre a equação paramétrica da reta tangente a curva no instante .
b) Suponha que no instante a partícula sai pela tangente em movimento retilíneo uniforme. Ache a posição da partícula no instante .
Ver solução completaQuestão 34
Encontre a equação da reta tangente da curva parametrizada por e no ponto . Faça a questão de duas maneiras: eliminando o parâmetro e sem eliminá-lo.
Ver solução completaQuestão 35
Considere a curva parametrizada por
(logarítimo na base ).
O ponto pertence a reta tangente a curva no ponto . Assinale o valor de :
Questão 36
Considere a curva com e a função . Suponha que e que para todo . Determine:
A equação da reta tangente a em .
Ver solução completaQuestão 38
Determine a equação na forma do plano tangente ao gráfico de no ponto .
Ver solução completaQuestão 39
6. Determine as equações da reta tangente e da reta normal à curva no ponto .
Ver solução completaQuestão 40
12. (1EE-2019.2) Considere a função
(a) Obtenha a equação da reta tangente ao gráfico de no ponto de abscissa .
Ver solução completaQuestão 42
12. (1EE-2019.2) Considere a função
(b) Existe uma outra reta s tangente ao gráfico de e que é paralela à reta do item anterior. Determine o ponto de tangência desta reta com o gráfico de
Ver solução completaQuestão 43
11. (1EE-2019.2) Considere a curva dada por .
(b) Encontre a equação da reta tangente à curva no ponto
Ver solução completaQuestão 44
(Capítulo 13.2 – Exercício 10)
Determine a derivada da função vetorial
Ver solução completaQuestão 45
4. Verifique se a curva parametrizada é regular no ponto . Se for, determine a equação da reta tangente a tal curva no ponto . Verifique também se a curva tem reta normal no ponto e determine a sua equação. Faça um esboço:
(a) , .
Ver solução completaQuestão 46
4. Verifique se a curva parametrizada é regular no ponto . Se for, determine a equação da reta tangente a tal curva no ponto . Verifique também se a curva tem reta normal no ponto e determine a sua equação. Faça um esboço:
(b) ,
Ver solução completaQuestão 47
5. Considere a curva parametrizada , . Verifique se tal curva admite reta tangente paralela ao vetor . Se sim, em qual(quais) ponto(s) da curva isso ocorre?
Ver solução completaQuestão 48
Considere a curva parametrizada por , onde é uma constante. Para que valor de a reta tangente a no ponto passa pelo ponto ?
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 49
Considere a curva definida pela função vetorial
onde .
Encontre equações simétricas para a reta tangente à curva no ponto .
Ver solução completaQuestão 50
Considere a curva , , e o triângulo delimitado pelas retas tangentes a nos pontos . A área deste triângulo é:
Escolha uma opção:
11
33/4
99/2
11/2
99/4
Ver solução completaQuestão 51
2.2. Ache os pontos do hiperboloide nos quais a reta normal é paralela à reta que une os pontos e .
Ver solução completaQuestão 52
Considere a esfera e a parte de cone com . Seja a curva dada pela intersecção destas superfícies.
- Determine uma parametrização para a curva , explicitando seu domínio.
- Escreva a equação da reta tangente à curva no ponto .
- Determine os pontos sobre a curva mais distantes da origem.
Questão 53
Encontre as equações paramétricas para a reta tangente à curva definida pela interseção das superfícies e no ponto de coordenadas .
Ver solução completaQuestão 54
Considere a curva parametrizada espacial
Calcule e a equação paramétrica da reta tangente ao traço de em .
Ver solução completaQuestão 55
Sejam e e duas funções vetoriais. Considere a curva definida por
- Encontre a função vetorial . Ou seja, calcule o produto vetorial acima.
- Encontre equações paramétricas para a reta tangente à curva no ponto .
- Calcule a curvatura de mesmo ponto .
Questão 56
Seja a curva fechada dada pela interseção das superfícies de equações cartesianas e (Fig. 1).
Determine os pontos da curva onde a reta tangente é horizontal (paralela ao plano ).
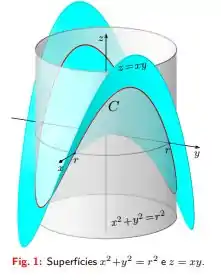
Questão 57
(Capítulo 13.2 – Exercício 2)
(a) Faça um esboço grande da curva descrita pela função vetorial , e desenhe os vetores e .
(b) Desenhe o vetor começando em (1, 1) e compare com o vetor
Explique porque esses vetores estão tão próximos um do outro tanto em módulo quanto em direção e sentido.
Ver solução completa