Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.4 - Ex. 10

Calcule a integral dada, colocando-a em coordenadas polares.

∫ ∫ R x + y   d A ,

onde R é a região que está a esquerda do eixo y e entre as circunferências x 2 + y 2 = 1 e x 2 + y 2 = 4 .

Passo 1

OIÊ, vamos lá. Quando mudamos para coordenadas polares a integral passa a ter outro formato. Substituímos o d A e as variáveis da função ela fica assim :

∫ ∫ R f ( r , θ )     r   d r   d θ

Então nessa questão precisamos descobrir primeiro como ficará a função escrita em coordenadas polares

f ( x , y )   = x + y

⇒ f ( r , θ ) =   ? ?

O próximo passo que iremos fazer é entender quem é a região R e quais serão os limites de integração.

Com todas essas informações definidas poderemos calcular a integral.

Bora começar!

Passo 2

Para transformar a integral em coordenadas polares, usamos:

x = r c o s θ             e         y = r   s e n   θ

Assim,como a função era :

f ( x , y )   = x + y

Iremos substituir os novos valores de x   e   y

f ( r , θ )   =   ( r c o s θ   + r   s e n   θ )  

f ( r , θ )   =   r ( c o s θ   +   s e n   θ )  

Reescrevendo na integral , teremos::

∫ ∫ R x + y   d A = ∫ ∫ R r c o s   θ   + s e n   θ ⋅ r   d r   d θ

Nunca esqueça do jacobiano r quando passamos para coordenadas polares!

Passo 3

Agora que já reescrevemos a função, vamos achar a região R.

O enunciado nos informa que a região R está a esquerda do eixo y e entre as circunferências x 2 + y 2 = 1 e x 2 + y 2 = 4 .

Vamos relembrar um conceito importante. Representamos uma circunferência através da seguinte equação :

( x - x 0 ) 2 + ( y - y 0 ) 2 = r 2

onde :

( x 0 , y 0 ) = Pontos do centro da circunferência

r = raio

Quando a equação tem o formato:

x 2 + y 2 = r 2

quer dizer que os pontos do centro da circunferência são ( 0,0 )

Logo podemos afirmar as seguintes informações das equações dadas :

→   x 2 + y 2 = 1 (I)

r 2 = 1

r = 1

r = 1

(I) possui raio igual a 1 e os pontos do centro da circunferência serão ( 0,0 ) .

→ x 2 + y 2 = 4 (II)

r 2 = 4

r = 4

r = 2

(II) possui raio igual a 2 e os pontos do centro da circunferência serão ( 0,0 ) .

Show, já sabemos as duas circunferências porém um detalhe importante é que a região R entre ela e à esquerda delas . Desenhando encontraremos a seguinte figura:

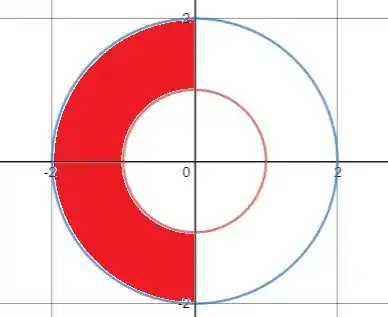
Passo 4

Para encontrarmos os limites temos que descobrir quanto r e θ variam.

Vamos começar pelo r :

Aqui nós queremos apenas saber o quanto o raio vai variar. Nos passos anteriores vimos que teremos dois círculos um de r = 1 (I) e outro de r = 2 . Então esses serão nossos limites em r :

1 ≤ r ≤ 2

Agora vamos ver o de θ . Aqui nós vamos delimitar em que parte do círculo vamos integrar. Lembra que na figura anterior ficamos apenas com a parte esquerda do círculo? Isso quer dizer que a variação será entre os ângulos π 2 e   3 π 2 .

π 2 ≤ θ ≤ 3 π 2

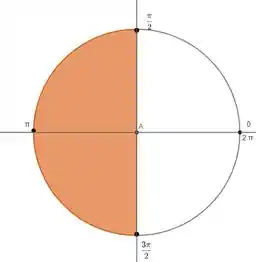
Lembrando dos ângulos de um círculo:

Passo 5

Oba, já a mudamos para as coordenadas polares e encontramos a região R. Vamos então substituir tudo na integral e começar os cálculos :

→ ∫ ∫ R f ( r , θ )     r   d r   d θ

Revisando as informações que encontramos :

⇒ 1 ≤ r ≤ 2

⇒ π 2 ≤ θ ≤ 3 π 2

⇒ f ( r , θ ) = r c o s   θ   + s e n   θ ⋅

Substituindo :

∫ π / 2 3 π / 2 ∫ 1 2 r c o s c o s   θ   + s e n   θ ⋅ r   d r   d θ

Note que as integrais em r e θ são independentes, de modo que podemos escrevê-la da seguinte forma :

∫ ∫ R x + y   d A = ∫ π / 2 3 π / 2 c o s c o s   θ   + s e n   θ   d θ ⋅ ∫ 1 2 r 2   d r

Vamos fazer a integral separadamente para facilitar a nossa compreensão.Começando pela primeira :

→ ∫ π / 2 3 π / 2 c o s   θ   + s e n   θ   d θ

s e n   θ - c o s   θ   π 2 3 π 2

s e n 3 π 2 - c o s   3 π 2   - s e n π 2 + c o s   π 2  

- 1 - 0   - 1 + 0  

∫ π / 2 3 π / 2 c o s   θ   + s e n   θ   d θ =   - 2

Agora vamos para a segunda :

→ ∫ 1 2 r 2   d r

r 3 3 1 2

8 3 - 1 3

∫ 1 2 r 2   d r = 7 3

Multiplicando os resultados :

∫ π / 2 3 π / 2 c o s c o s   θ   + s e n   θ   d θ ⋅ ∫ 1 2 r 2   d r

( - 2 )   . 7 3  

Portanto,

∫ ∫ R x + y   d A = - 14 3

Resposta

- 14 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Usando coordenadas polares, calcular:f) int_0^(sqrt(2)) int_y^(sqrt(4 - y^2)) x d x d y
Calcular ∬_R^() sqrt(x^2 + y^2) d x d y , sendo R a região delimitada por x^2 + y^2 = 1 e x^2 + y^2 = 9 .
Calcular ∬_R^() x d x d y , sendo R a região delimitada por x^2 + y^2 - 4 x = 0 .
Usando coordenadas polares, calcular:g) int_0^2 int_0^y x d x d y
Calcular ∬ R ( x 2 + y 2 ) d x d y , sendo R é dada por:a) Círculo centrado na origem de raio a .