Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.1 - Ex. 11
- Elimine o parâmetro para encontrar uma equação cartesiana da curva:
- Esboce a curva e indique com uma seta a direção na qual a curva é traçada quando o parâmetro aumenta.
Passo 1
Fala pessoal! De boa?
Essa questão pede para determinarmos a equação cartesiana de uma curva parametrizada pelas seguintes equações, . Além disso, deseja-se esboçar a curva no plano cartesiano e indicar a direção na qual a curva é traçada à medida que o parâmetro aumenta.
E o que podemos fazer para resolver?
- Identificar as equações paramétricas.
- Eliminar o parâmetro como a identidade trigonométrica
Fazer o esboço e analisar a direção a trajetória a partir do intervalo dado .
Vamos começar!
Passo 2
a) Para “isolar” o parâmetro no caso em que temos seno e cosseno, usamos a relação fundamental da trigonometria:
Temos e com essa identidade, obtemos:
Esta é a equação de um círculo de raio centrado na origem do sistema de coordenadas cartesianas.
Passo 3
b) Por mais que a equação gerada sea de uma circunfêrencia de raio . O intervalo de parametrização indica que estamos falando de apenas etada dela.
Podemos descobrir seu início e seu fim, substituindo o intervalo nas equações de e .
Para temos
Para temos
Assim, nossa semicircunferência começa no ponto e termina no ponto .
Além disso, nesse intervalo de temos que
Então
E nossa semicircunferência está na parte positiva do eixo .
Passo 4
Traçando nossa curva, temos
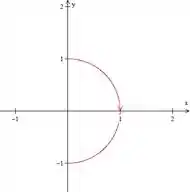
A direção na qual a curva é traçada conforme o parâmetro aumenta é no sentido anti-horário ao redor do círculo. Isso significa que à medida que aumenta de para , a curva percorre o círculo no sentido de para , começando do ponto (quando ) e terminando no ponto (quando ).
Resposta
