Descrever analítica e graficamente uma função tal que não existe e existe.
Passo 1
Falaee, tranquilinho?? Queremos mostrar de forma analítica (ou seja, por cálculos) e de forma gráfica uma função que atenda os seguintes requisitos:
1) não existe;
2) existe.
Então galera, antes começar a resolução vale ressaltar que existem INFINITOS exemplos de funções que atendem as características dadas pelo enunciado, tudo bem? O que vamos fazer aqui é utilizar apenas uma, que já será o suficiente!
Para isso, lembre-se que, para um limite existir em um ponto , então os limites laterais em torno desse ponto devem ser iguais, ou seja:
Se
Então:
Agora bora lá!!
Passo 2
A primeira característica que a função tem que ter é ter os limites laterais quando diferentes, ou seja, quando pela direita tem que ser diferente quando pela esquerda, então podemos pegar uma função constante qualquer, tal como:
Essa é a primeira característica, ok? Então vamos para a próxima!
Passo 3
A segunda característica que a função tem que ter é ter os limites laterais quando iguais, ou seja, quando pela direita tem que ser igual quando pela esquerda, então podemos pegar uma função qualquer que existe em , se liga:
Essa descrição foi a parte analítica da coisa, tudo bem galera? Para facilitar a visualização, podemos escrever as funções assim ó:
Com isso, perceba que:
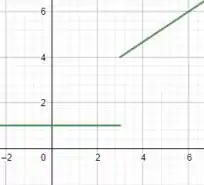
Por fim, fazendo a descrição gráfica, ou seja, plotando o gráfico dessas funções, teremos:
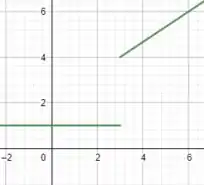
Note que os limites laterais em torno de são diferentes (note o salto dafunção nesse ponto!!).
Por outro lado, veja que em o limite existe pois se você ir se aproximando de tanto pela esquerda quanto pela direita, você terá um mesmo valor !!
Passo 4
Se ainda não percebeu de forma analítica que o limite existe em vamos fazer o seguinte... vamos pegar dois números muuuito próximos de , onde um se aproxima pelos números maiores que (por exemplo: ) e outro que se aproxima por números menores (por exemplo: ).
Fazendo :
Fazendo :
Note que os resultados são muuuito próximos de !!
Isso significa que o limite existe nesse ponto!!
E está aí nossas descrições! 😊
Resposta