Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.6 - Ex. 3
Determine a área da superfície.
A parte do plano que está no primeiro octante.
Passo 1
Faala, pessoal!
Essa questão pede pra gente calcular a área de uma superfície que ela descreveu.
Vamos usar essa fórmula aqui:
Onde é a área de uma superfície definida pelo gráfico de , em um domínio .
Então nosso objetivo é descobrir quem é , calcular as derivadas parciais, e substituir na fórmula. Aí, vamos definir o domínio e calcular a integral!
Passo 2
A nossa superfície é parte de um plano:
Vamos isolar o pra ter uma função :
Então vamos calcular as derivadas parciais.
Primeiro em função de , considerando constante:
Agora em função de , com constante:
Voltando pra nossa fórmula:
Resolvendo as contas:
Podemos tirar da integral, por ser constante:
E como a área de um domínio no plano é calculado assim:
A área da superfície fica:
Passo 3
Agora vamos ver o domínio .
Vamos desenhar nosso plano no primeiro octante:
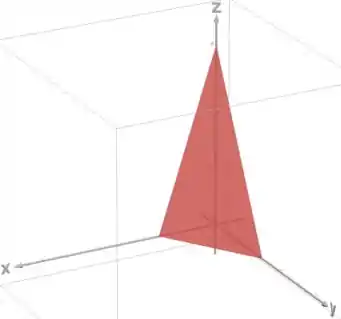
Pelo desenho, conseguimos ver que o domínio (que é a projeção de no plano ), fica um triângulo:
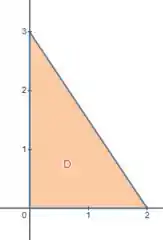
Como nós precisamos calcular a área desse domínio, usamos :
Então a área da superfície fica: