Determine se o conjunto dado é ou não: (a) aberto, (b) conexo e (c) simplesmente conexo.
Passo 1
Oie, gente, tudo certo??
Nessa questão, é dado um conjunto:
E precisamos descobrir se ele é aberto, conexo, e simplesmente conexo.
Tá... mas o que raios é isso??
Vamos lembrar essas definições:
- Aberto: para todo ponto do conjunto existe uma bola aberta centrada nesse ponto que esteja inteira no conjunto.
- Conexo: quaisquer dois pontos no conjunto podem ser ligados por um caminho inteiro dentro do conjunto.
- Simplesmente conexo: é conexo, e qualquer curva fechada contorna só pontos que estejam dentro do conjunto.
Na prática, quer dizer que as curvas que limitam o conjunto não pertencem a ele:
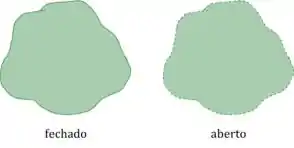
Na prática, o conjunto não é constituído de dois ou mais pedaços separados.
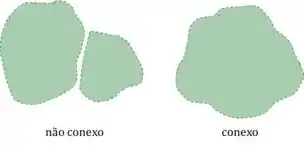
Na prática, além de ser conexo, não tem nenhum buraco no conjunto.
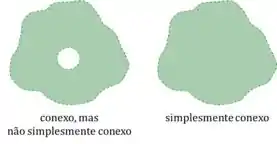
Então, a gente vai começar desenhando o nosso conjunto no , pra conseguir comparar com essas definições que acabamos de ver!
Daí vemos uma por uma se nosso conjunto se encaixa ou não nas definições.
Vamos?
Passo 2
O conjunto é
Essas expressões com dizem pra gente que estamos falando de regiões circulares! São três circunferências que definem :
Os casos estamos dentro do círculo. Já pra estamos fora do círculo.
Ou seja: estamos dentro de um círculo de raio , ou entre um círculo de raio e outro de raio , e as três circunferências estão incluídas, então:
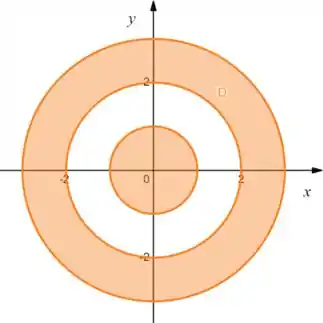
Passo 3
(a)
Nesse nosso conjunto, as curvas que limitam são as três circunferências. Olhando pro desenho e pras expressões, percebe que todas são “” ou “”, então o conjunto inclui essas curvas! Dessa forma:
Não, o conjunto não é aberto.
Passo 4
(b)
Só de olhar pro desenho a gente já vê que temos dois pedaços separados: um círculo e uma coroa circular... como ele não é uma região única,
Não, o conjunto não é conexo.
Passo 5
(c)
E aqui nem precisamos perder muito tempo – se não é conexo, não é simplesmente conexo:
Não, o conjunto não é simplesmente conexo.
Resposta
- Não
- Não
- Não