Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.1 - Ex. 14
- Elimine o parâmetro para encontrar uma equação cartesiana da curva:
- Esboce a curva e indique com uma seta a direção na qual a curva é traçada quando o parâmetro aumenta.
Passo 1
Fala pessoal. Tranquilo? Nossa missão nessa questão é determinar a equação cartesiana de uma curva parametrizada pelas seguintes equações, e . Além disso, deseja-se esboçar a curva no plano cartesiano e indicar a direção na qual a curva é traçada à medida que o parâmetro varia de a .
E o que podemos fazer para resolver?
- Identificar as equações paramétricas.
- Eliminar o parâmetro como a identidade trigonométrica
- Fazer o esboço e analisar a direção a trajetória a partir do intervalo dado
Vamos começar!
Passo 2
a) Para “isolar” o parâmetro no caso em que temos seno e cosseno, usamos a relação fundamental da trigonometria:
Assim
Esta é uma equação de uma hipérbole.
Passo 3
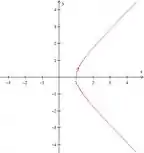
b) Por mais que a equação gerada sea uma hipérbole, pelo intervalo dado, percebemos que não estamos falando de uma hipérbole completa. Apenas de uma parte dela.
Temos que
Logo
Portanto, estamos falando do ramo da hipérbole que está na parte positiva do eixo .
Além disso, essa hipérbole tem foco no ponto .
Passo 4
Para a construção da curva. Podemos concluir que :
- A equação cartesiana da curva é .
- A curva é uma hipérbole que se aproxima das assíntotas e .
- A direção do traçado é da esquerda para a direita confirma aumenta.
Temos então o gráfico!
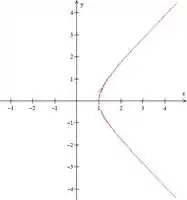
Resposta
