Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.4 - Ex. 29

Encontre a área da região que está dentro das duas curvas:

Passo 1

Olá! Hoje o dia está lindo para calcular uma bela integral de área.

Vamos começar?

Na questão teremos que esboçar o gráfico, pois com ela teremos uma noção de qual área calcular, além dos limites de integração.

A região de interseção se encontra entre as duas curvas na imagem abaixo:

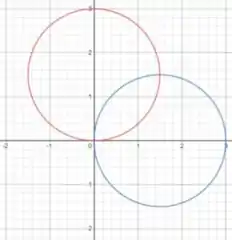
Passo 2

Vamos Definir os limites de integração?

Para a região no primeiro quadrante foi escolhido o intervalo de a , porque estamos interessados na área entre as duas curvas, apenas até o ponto onde as curvas e se interceptam pela primeira vez no primeiro quadrante.

As curvas se interceptam quando for igual a , o que acontece em no primeiro quadrante. Por isso os limites irão de a e de a .

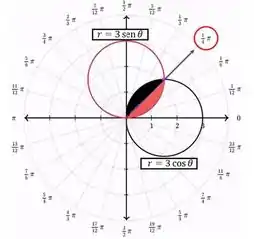
Passo 3

Agora que sabemos como é a região e seus limites de integração. Mãos a obra!

Vamos utilizar a equação da definição do cálculo da área polar.

E vamos dividi-la em duas partes, uma para a função (representada pela cor vermelha no gráfico) e outra para (representada pela cor preta no gráfico).

Podemos escolher apenas uma integral para resolver, pois as regiões são simétricas. Sendo assim é mais prático resolvermos e no final multiplicarmos por 2.