Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.3 - Ex. 56
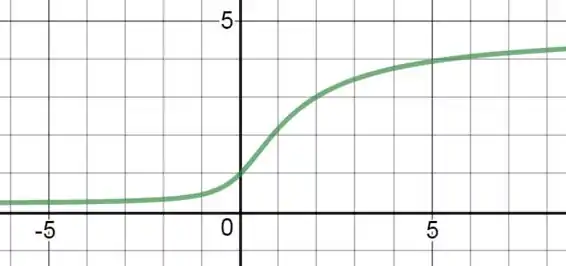
(a) Encontre as assíntotas vertical e horizontal.
(b) Encontre os intervalos nos quais a função é crescente ou decrescente.
(c) Encontre os valores máximos e mínimos locais.
(d) Encontre os intervalos de concavidade e os pontos de inflexão.
(e) Use a informação das partes (a)-(d) para esboçar o gráfico de .
Passo 1
Oie, bora resolver essa junto comigo?
(a) Para encontrar as assíntotas vertical e horizontal, primeiro, vamos analisar o comportamento da função para valores grandes de x e para x se aproximando de .
Assíntotas Verticais: Assíntotas verticais ocorrem quando o denominador de uma função se aproxima de zero. No caso de
A função possui uma assíntota vertical em
Pois a tangente é indefinida nessas posições.
Como a exponencial de qualquer número real é sempre positiva, a função não possui assíntotas verticais.
Passo 2
Assíntotas Horizontais: Para analisar as assíntotas horizontais, observe o comportamento da função para tendendo ao infinito.
Quando se aproxima de , se aproxima de
E
Se aproxima de
Passo 3
Como
é finito, a função possui assíntotas horizontais em
Passo 4
(b) Para determinar os intervalos de crescimento e decrescimento, precisamos encontrar onde a derivada da função é positiva (crescente) ou negativa (decrescente).
A derivada da função
Em relação a pode ser encontrada usando a regra da cadeia e é dada por:
Esta derivada é sempre positiva para todos os valores de exceto para onde é indefinida.
Portanto, a função é crescente em todo o seu domínio, exceto em onde é descontínua.
Passo 5
(c) Para encontrar os valores máximos e mínimos locais, precisamos encontrar os pontos críticos da função. Como a função é crescente em todo o seu domínio, não há valores máximos ou mínimos locais.
Passo 6
(d) Para determinar os intervalos de concavidade e os pontos de inflexão, precisamos encontrar a segunda derivada da função.
A segunda derivada da função
em relação a pode ser encontrada usando a regra do produto e é dada por:
A segunda derivada é positiva para e negativa para
Portanto, a função é côncava para baixo em côncava para cima em e novamente côncava para baixo em
Os pontos de inflexão ocorrem nos pontos onde a concavidade muda, que são
Passo 7
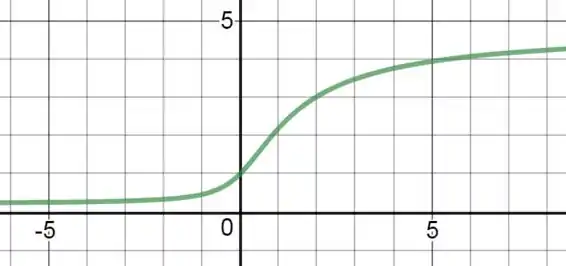
(e) Esboço do Gráfico
Pelas informações obtidas temos o gráfico:
Resposta
(a)
E
(b) é crescente em todo o seu domínio.
(c) não possui máximo nem mínimo local.
(d) possui concavidade para cima em valores de no intervalo e concavidade para baixo em . Então, o ponto de inflexão é em .
(e)
