(a) Encontre os intervalos de aumento ou diminuição.
(b) Encontre os valores máximos e mínimos locais.
(c) Encontre os intervalos de concavidade e os pontos de inflexão.
(d) Use as informações das partes para esboçar o gráfico.
Passo 1
Fala aí, tudo belezinha com você?
Bom, essa questão dá pra gente a função
E teremos que dizer algumas coisas sobre ela.
No item (a) precisamos encontrar os intervalos nos quais a função é crescente ou decrescente.
Para saber isso podemos usar as informações dadas pela derivada da função, pois ela representa a inclinação da reta tangente ao gráfico da função. Assim, se
Significa que a função é crescente, já que a reta tangente tem derivada positiva. E se
A função é decrescente, já que a derivada é negativa.
No item (b), queremos encontrar os valores de máximo e mínimo locais.
Para isso também usamos a ideia dada pela inclinação da reta tangente. Ou seja, a derivada. Assim:
Teremos um ponto de máximo ou mínimo da função, já que a inclinação da reta tangente será nula.
No item (c) vamos encontrar os intervalos de concavidade e os pontos de inflexão.
E aqui faremos uso da derivada segunda. Sabendo que se:
Nossa curva terá concavidade para baixo.
E se
E nossa curva terá concavidade para cima.
E finalmente, no item (d) vamos usar as informações das partes (a)-(c) para esboçar o gráfico de .
Agora que já sabemos o que fazer em cada item, vem comigo que te mostro como vai ficar tudo isso.
Passo 2
Vamos resolver por ordem dos itens, beleza?
Nossa função é:
Vamos começar derivando ela, usando a regra da derivada composta:
Ou seja, a derivada de uma função com outra dentro é o produto da derivada de cada uma das funções, na função do problema, as funções são:
Passo 3
Beleza, a gente vai usar a regra geral para calcular as derivadas de e :
E:
Agora, vamos aplicar a regra da derivada composta:
Passo 4
Show de bola, bora analisar então quando a derivada é positiva e negativa, porque isso vai dizer pra gente quando a função aumente e diminui.
Como o denominador da derivada tem apenas elevado , então o denominador vai sempre ser positivo e para saber se a derivada vai ser positiva ou negativa, vai depender apenas do numerador que é:
Que vai ser positivo quando , negativo quando e igual a quando .
Assim a gente conclui que:
(a) A função aumenta nos intervalos e diminui em .
Passo 5
Com a gente derivada também a gente encontra os máximos e mínimos locais, que vão acontecer quando :
Logo:
(b) , é o ponto de mínimo.
De mínimo, pois para valores de a derivada é negativa e para valores de é positiva.
Passo 6
Bom, para sabermos sobre os intervalos de concavidade e os pontos de inflexão, a gente vai pegar a segunda derivada usando a regra da derivada de divisão de funções:
A gente iguala a :
E encontramos:
E então:
(c) Concavidade para cima , concavidade para baixo e os pontos de inflexão são e .
Passo 7
(d)
Vimos que nossa função aumenta nos intervalos e diminui em .
, é o ponto de mínimo.
Concavidade para cima , concavidade para baixo e os pontos de inflexão são e .
E com isso, podemos plotar o gráfico da função :
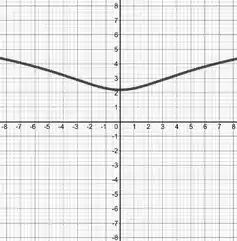
Prontinho.
Resposta
(a) A função aumenta nos intervalos e diminui em .
(b) , é o ponto de mínimo.
(c) Concavidade para cima , concavidade para baixo e os pontos de inflexão são e .