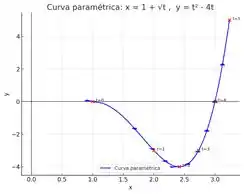
Esboce a curva usando as equações paramétricas para marcar os pontos. Indique com uma seta a direção na qual a curva é traçada quando aumenta.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado quer que a gente esboce a curva dada pelas equações paramétricas abaixo, indicando com setas a direção na qual aumenta:
Bom, para fazer isso, vamos criar uma tabelinha de valores, calculando alguns pontos-chave no intervalo e, em seguida, traçar a curva indicando sua direção.
Passo 2
Vamos começar calculando as coordenadas para valores inteiros de no intervalo :
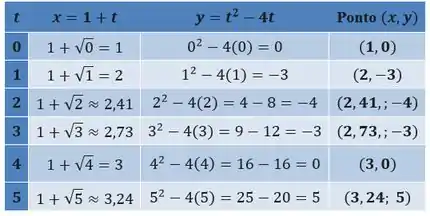
Então, o ponto inicial da curva é (para ) e o ponto final é (para ).
Passo 3
Para ter uma ideia mais clara do formato, podemos tentar eliminar o parâmetro . Assim, de , isolamos :
Como e , o domínio de é .
Então, elevamos ao quadrado para encontrar :
(Isso só é válido no domínio ).
E substituímos na equação de :
Esta é a equação de uma parábola de grau em relação a .
Passo 4
A direção vai ser determinada pelo aumento de e conforme aumenta.
Pra analisar o movimento em , olhamos pra equação . Como sempre aumenta com , o valor de sempre aumenta de a aproximadamente . Então, a curva se move sempre para a direita.
O movimento em é analisado por . Esta é uma parábola com vértice em . Então,
- Para , diminui (de a )
- Para , aumenta (de para ).
O ponto mais baixo da curva (mínimo de ) ocorre em , no ponto .
Passo 5
Então, a gente já sabe que o esboço da curva parte do ponto , desce até o ponto e, em seguida, sobe até o ponto .
Assim, nosso gráfico vai ficar:
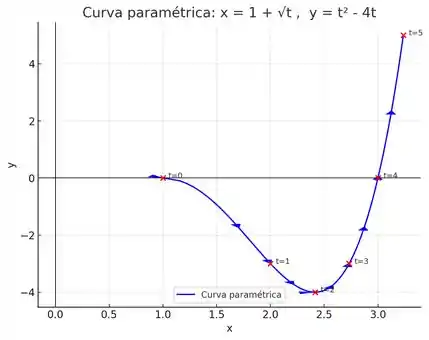
Valeu, galera! Até a próxima! 😉
Resposta