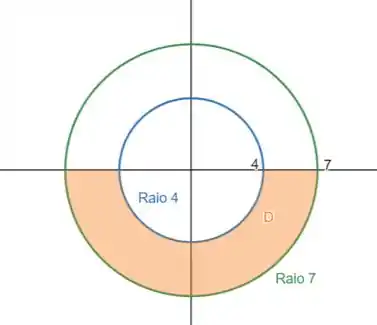
Esboce a região cuja área é dada pela integral e calcule-a.
Passo 1
Faala, pessoal!
Nessa questão, temos uma integral:
Que representa a área de uma região.
Precisamos esboçar essa região e calcular a integral!
Pra isso, vamos lembrar que a área de uma região pode ser calculada assim:
E que quando fazemos uma mudança para coordenadas polares , temos o jacobiano , então:
Vamos usar isso pra determinar a região que nossa integral representa!
Depois, vamos calcular a integral iterada, de dentro pra fora.
Passo 2
Nossa integral é:
Como vimos, ela representa a área de uma região :
Só que o integrando já é o mesmo da definição de área, então a região é definida pelos limites de integração:
Os limites de indicam que estamos no terceiro ( até ) e quarto ( até ) quadrantes.
E os limites de indicam que estamos entre duas circunferências: uma de raio e outra de raio .
Então:
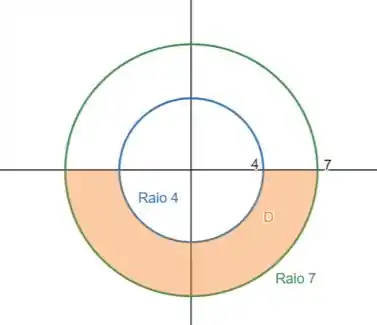
Passo 3
Agora vamos calcular a integral, de dentro pra fora.
Primeiro em função de , considerando como constante:
Substituindo os limites de integração:
E agora integramos em função de :
Então, achamos o valor da integral:
Resposta