Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.1 - Ex. 4

(a) Estime o volume do sólido que está abaixo da superfície z = 1 + x 2 +   3 y e acima do retângulo R = 1,2 × [ 0,3 ] . Use a soma de Riemann com m = n = 2 e escolha os pontos de amostragem como os cantos inferiores esquerdos.

(b) Use a Regra do Ponto Médio para estimar o volume do item (a).

Passo 1

Faaaaaala turminha, tudo bem com vocês?

Vamos começar entendo o enunciado, beleza?

Precisamos estimar o volume que está abaixo de uma superfície z e acima de uma retângulo R através da soma de Riemann. E também estimar o volume através da Regra do Ponto Médio.

Como fazer isso?

Primeiro vale reforçar que z = f ( x , y ) , e a representação do retângulo é equivalente a

O volume através da soma de Riemann é

V ≈ ∑ i = 1 m ∑ j = 1 n f x i j , y i j Δ A

Sabendo disso, devemos esboçar o gráfico da região do retângulo e determinar os pontos inferiores esquerdos, e determinar a área Δ A . Agora, podemos expandir o somatório, até m = n = 2 e aplicar os pontos encontrados na função f x i j , y i j , logo vamos obter o volume.

Agora para estimar pela regra do ponto médio, vamos aplicar o mesmo método de antes, porém temos que considerar nos pontos o centro de cada quadrado do esboço da região do retângulo.

Partiu resolver essa! Vamos tirar de letra agora!

Passo 2

Letra (a):

Vamos primeiro construir a área delimitada pela região R e os pontos que serão usados na função.

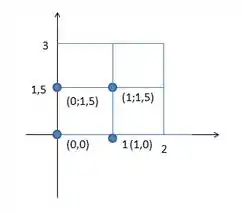
x é entre 1 ≤ x ≤ 2 e está dividido em m = 2 espaços. Já em y temos o intervalo de 0 ≤ y ≤ 3 e está dividido em n = 2 . Logo, o gráfico desses pontos é:

Como devemos considerar os cantos inferiores esquerdos, então os pontos vão ser:

0 ; 0 ; 1 ; 0 ; ( 0 ; 1,5 ) ; ( 1 ; 1,5 )

E o valor de Δ A ?

É a área de cada um dos retângulos. Cada um deles tem base 1 e altura 1,5 , logo:

Δ A = 1.1,5 = 1,5

Passo 3

Agora vamos estimar o valor do volume usando a fórmula de Riemann.

Vamos lembrar da fórmula, já aplicando m = n = 2 . Temos:

V ≈ ∑ i = 1 2 ∑ j = 1 2 f x i j , y i j Δ A

Expandindo esse somatório, vamos ter:

V ≈ f x 11 , y 11 Δ A + f x 12 , y 12 Δ A + f x 21 , y 21 Δ A + f x 22 , y 22 Δ A

Mas lembra que já obtemos esses pontos antes:

0 ; 0 ; 1 ; 0 ; ( 0 ; 1,5 ) ; ( 1 ; 1,5 )

Logo, vamos aplicar:

V ≈ f 0 ; 0 Δ A + f 1 ; 0 Δ A + f 0 ; 1,5 Δ A + f 1 ; 1,5 Δ A

Já sabemos que Δ A = 1,5 .

E agora vamos aplicar os pontos na função f x , y = 1 + x 2 +   3 y . Assim, temos:

f 0 ; 0 = 1 + 0 2 +   3 0 = 1

f 1 ; 0 = 1 + 1 2 +   3 0 = 2

f 0 ; 1,5 = 1 + 0 2 +   3 1,5 = 5,5

f 1 ; 1,5 = 1 + 1 2 +   3 1,5 = 6,5

Logo, o volume será:

V ≈ Δ A   f 0 ; 0 + f 1 ; 0 + f 0 ; 1,5 + f 1 ; 1,5

V ≈ 1,5 1 + 2 + 5,5 + 6,5 ≈ 22,5

Passo 4

Letra (b):

Agora o problema pede para usarmos a regra do ponto médio.

Mas repare que a área de cada retângulo continua a mesma, o que muda são os pontos que vamos usar, os pontos médios de cada retângulo.

Saca só nesse desenho dos pontos:

Veja que os pontos médios são:

1 2 , 3 4 ; 3 2 , 3 4 ; 3 2 , 9 4 ; 1 2 , 9 4

Passo 5

Agora vamos aplicar a regra do ponto médio para a mesma função:

f x , y = 1 + x 2 +   3 y

V ≈ ∑ i = 1 2 ∑ j = 1 2 f x - , y - Δ A

O processo vai ser similar ao que fizemos antes, porem com os pontos diferentes.

Assim temos,

V ≈ f x 11 , y 11 Δ A + f x 12 , y 12 Δ A + f x 21 , y 21 Δ A + f x 22 , y 22 Δ A

V ≈ f 1 2 , 3 4 Δ A + f 3 2 , 3 4 Δ A + f 3 2 , 9 4 Δ A + f 1 2 , 9 4 Δ A

Aplicando os pontos na função teremos:

f 1 2 , 3 4 = 1 + 1 2 2 + 3 3 4 = 7 2

f 3 2 , 3 4 = 1 + 3 2 2 + 3 3 4 = 11 2

f 3 2 , 9 4 = 1 + 3 2 2 + 3 9 4 = 10

f 1 2 , 9 4 = 1 + 1 2 2 + 3 9 4 = 8

Assim, nosso volume fica:

V ≈ Δ A f 1 2 , 3 4 + f 3 2 , 3 4 + f 3 2 , 9 4 + f 1 2 , 9 4

Sabendo que Δ A = 1,5 , temos o volume como:

V ≈ 1,5 7 2 + 11 2 + 10 + 8

V ≈ 40,5

Resposta

a ) 22,5

b ) 40,5

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a integral iterada.int_0^1 int_0^1 sqrt(s + t) d s d t
Calcule a integral dupla, identificando-a antes com o volume de um sólido. ∬ R 2d A ,R = { ( x , y ) | 2 ≤ x ≤ 6 ;- 1 ≤ y ≤ 5 }
Calcule a integral iterada.int_0^1 int_0^1 (x + y)^2 d x d y
Calcule a integral iterada.int_1^4 int_1^2 ((x)/(y) + (y)/(x)) d y d x
Calcule a integral iterada.int_0^1 int_1^2 ( x + e^(- y) ) d x d y