Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.5 - Ex. 37

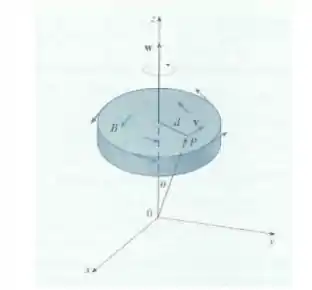
Este exercício ilustra a relação entre o vetor rotacional e rotações. Seja B um corpo rígido girando em torno do eixo z . A rotação pode ser descrita pelo vetor ω → = ω k → , onde ω é a velocidade angular de B , ou seja, a velocidade tangencial de qualquer ponto P em B dividido pela distância d do eixo de rotação. Seja r → = x , y , z o vetor posição de P .

  1. Considerando o ângulo θ da figura, mostre que o campo de velocidades de B é dado por v → = ω → × r →
  2. Mostre que v → = - ω y j → + ω x j →
  3. Mostre que r o t   v → = 2 ω →

Passo 1

Oi, galera! Tudo bem?

A questão tem 3 partes: a primeira quer que a gente mostre que o campo de velocidades de B , que é nosso corpo rígido girando em torno de z da figura, é:

v → = ω → × r →

onde ω é a velocidade angular de B e r → o vetor posição de qualquer ponto P . Para isso vamos partir da informação que o enunciado deu de que a velocidade é angular é a velocidade tangencial dividida pela distância do eixo de rotação.

A parte b) pede para que a gente mostre que:

v → = - ω y j → + ω x j →

Para isso, vamos calcular o produto vetorial entre ω → × r → .

Por último, temos a parte c), que pede que a gente chegue em:

r o t   v → = 2 ω →

E para isso é só calcularmos o rotacional do vetor v → , que é dado na letra b).

Vamos lá!

Passo 2

  1. Bom, precisamos chegar em:

    2. v → = ω → × r →

    Admitindo que a distância da origem até o ponto P é r , então pelo desenho:

    d = r s e n ( θ )

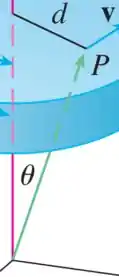
    O enunciado diz que a velocidade é angular é a velocidade tangencial dividida pela distância do eixo de rotação, então:

    ω = v d

    Isolando v :

    v = ω d

    Agora podemos substituir a relação que encontramos pela imagem:

    v = ω r s e n ( θ )

    E esse é justamente o módulo do produto vetorial entre os vetores ω → e r → , uma vez que θ é o ângulo entre eles! Saca só:

    v → = ω �� × r →

    Chegamos no que o enunciado pediu!

    Passo 3

  2. Para o item b ) , precisamos mostrar que o vetor v → é:

    3. v → = - ω y j → + ω x j →

    Mas sabemos que:

    v → = ω → × r →

    Então, preciso resolver o produto vetorial entre ω → e r → para chegar em v → .

    Retomando os dados do enunciado:

  • Velocidade angular: ω → = ω k → = 0,0 , ω

  • Posição: r → = x , y , z

Agora podemos calcular o produto vetorial entre eles:

v → = ω → × r → = i → j → k → 0 0 ω x y z

Para cada componente i , j e k , temos que multiplicar a matriz que achamos tirando a linha e a coluna da componente que estamos procurando.

v → = ω → × r → = 0 ω x y i - 0 ω x z j + 0 0 x y k

Depois, tiramos o determinante de cada matriz e ficamos com:

v → = ω → × r → = i → - ω y + j → ω x + 0 k →

Assim o vetor v → é:

v → = - ω y i → + ω x j →

Passo 3

  • Legal! Chegamos na última parte. O próximo passo é calcular o rotacional de v → . Já estamos carecas de saber como se calcula o rotacional, então, fazendo o processo de produto vetorial que fizemos no passo anterior:

    • ∇ × v → = i → j → k → ∂ ∂ x ∂ ∂ y ∂ ∂ z - ω y ω x 0

    = i → ∂ ∂ y 0 - ∂ ∂ z ( ω x ) + j → ∂ ∂ z ( - ω y ) - ∂ ∂ x 0 + k → ∂ ∂ x ( ω x ) - ∂ ∂ y ( - ω y )

    Como as derivadas parciais das componentes i →   e   j → são nulas, ficamos apenas com a componente k → :

    ∇ × v → = k → ∂ ∂ x ( ω x ) - ∂ ∂ y ( - ω y ) = 2 ω k → = 2 ω →

    Resposta

    ( a ) v → = ω → × r →

    ( b ) v → = - ω y i → + ω x j →

    c ∇ × v → = 2 ω →

    Ver Outros Exercícios desse livro

    Exercícios de Livros Relacionados

    Seja f um campo escalar e F um campo vetorial. Diga se cada expressão tem significado. Em caso negativo, explique por quê. Em caso afirmativo, diga se é um campo vetorial ou escalar. r o tf g r a df d
    Existe um campo vetorial G → em R 3 tal que rot ⁡ G → = x y z , - y 2 z , y z 2 ? Explique.
    Existe um campo vetorial G em R^3 tal que r o t G = 〈x sen y , cos y , z - x y〉 ? Explique.
    Determine se o campo vetorial é conservativo ou não. Se for conservativo, determine uma função f tal que F = ∇ f F x , y , z = y e - xi + e - x j + 2 zk
    Determine se o campo vetorial é conservativo ou não. Se for conservativo, determine uma função f tal que F = ∇ f F x , y , z = e zi + j + x e zk