Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 15.4 - Ex. 23

Nos Exercícios 23-26, esboce a região de integração e converta cada uma das integrais polares ou soma de integrais a uma integral cartesiana ou soma de integrais. Não calcule as integrais.

∫ 0 π 2 ∫ 0 1 r 3   s e n θ cos ⁡ θ d r   d θ

Passo 1

Faaaala, cara! Tranquileba?

Das coordenadas polares temos que:

x = r cos ⁡ θ

y = r   s e n θ

x 2 + y 2 = r 2

E em caso de dúvidas, vejamos a figura para que possamos entender melhor.

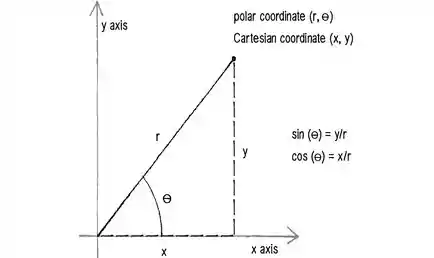
E em se tratando de integrais, quando transformamos uma integral para coordenadas polares, temos que adicionar o jacobiano das coordenadas polares, que no caso é r .

Passo 2

A forma mais fácil e mais rápida se de resolver problemas desse tipo, é fazendo um esboço. Por termos em coordenadas polares, podemos construir uma circunferência, isto é:

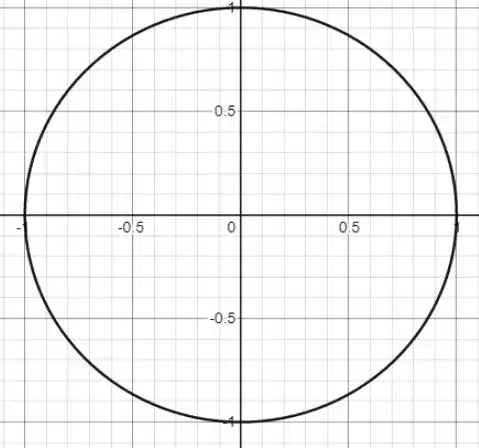
Dado pela limites de integração do enunciado que θ vai de [ 0 , π 2 ] e o raio é 1, temos:

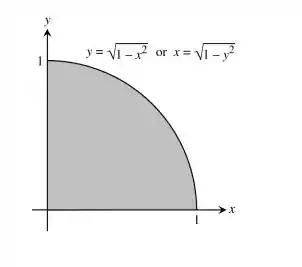
Passo 3

Dada a função:

r 3 s e n θ cos ⁡ θ

Lembrando que:

x = r cos ⁡ θ

y = r   s e n θ

Temos que:

r 3 s e n θ cos ⁡ θ = x y r

Onde esse r extra é o jacobiano que nos permitiu ates passar de coordenadas cartesianas opara a coordenadas polares, agira que estamos fazendo o caminho inverso ele deve ser retirado. Logo:

r 3 s e n θ cos ⁡ θ = x y

Assim, podemos expressar como:

∫ 0 π 2 ∫ 0 1 r 3   s e n θ cos ⁡ θ d r   d θ = ∫ 0 1 ∫ 0 1 - x 2 x y   d y   d x      

Ou:

∫ 0 π 2 ∫ 0 1 r 3   s e n θ cos ⁡ θ d r   d θ = ∫ 0 1 ∫ 0 1 - y 2 x y   d x   d y

Resposta

∫ 0 π 2 ∫ 0 1 r 3   s e n θ cos ⁡ θ d r   d θ = ∫ 0 1 ∫ 0 1 - x 2 x y   d y   d x      

Ou:

∫ 0 π 2 ∫ 0 1 r 3   s e n θ cos ⁡ θ d r   d θ = ∫ 0 1 ∫ 0 1 - y 2 x y   d x   d y

Exercícios de Livros Relacionados

Calcule a integral dada, colocando-a em coordenadas polares. ∬ De - x 2 - y 2d A , onde D é a região delimitada pelo semicírculo x = 4 - y 2 e o eixo y .
A região dentro do círculo x - 1 2 + y 2 = 1 e fora do círculo x 2 + y 2 = 1 .
Utilize a integral dupla para determinar a área da região.A região dentro do círculo r = 1 + cos ⁡ θ e r = 3 cos ⁡ θ .
Calcule o valor da integral múltipla. ∫ ∫ D xd A Onde D é a região do primeiro quadrante que se encontra entre os círculos x 2 + y 2 = 1 e x 2 + y 2 = 2 .
Descreva a região cuja área é dada pela integral ∫ 0 π 2 ∫ 0 s e n 2 θ rd rd θ