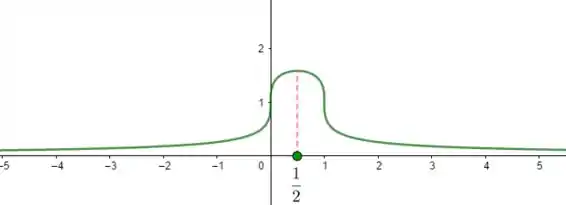
Faça o gráfico da função . Em seguida, use a primeira derivada da função para explicar o que você está vendo.
Passo 1
Inicialmente vamos considerar em seguida, manualmente ou com auxílio de algum software obteremos um gráfico parecido com o que está abaixo,
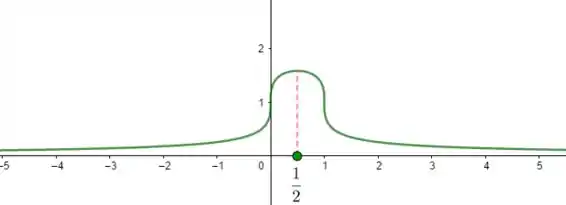
Passo 2
Agora, explicaremos o por que o gráfico ficou daquela forma.
Vejamos, inicialmente que o domínio de nossa função são todos os reais. E como não temos ninguém anulando o denominador, não há assíntota vertical.
Além disso, perceba que
Passo 3
Agora, vamos analisar outros fatos do gráfico: se há máximo, mínimo, etc. Precisaremos saber qual a cara de ou seja,
Utilizando a regra da diferença e a regra da cadeia teremos
Reescrevendo as potências teremos,
Sendo assim,
Passo 4
Sabemos que através de podemos encontrar pontos críticos e isso irá nos ajudar a explicar o que está acontecendo com o gráfico de . Dessa maneira, para encontrar pontos críticos precisamos que ,isto é,
Dividindo a igualdade por temos
Para que a fração seja igual a zero, precisamos que o numerador seja igual a zero, ou seja,
Pela propriedade de potência de potência
Aplicando a fórmula de Bhaskara, obteremos que a raízes do polinômio é .
Além disso, a derivada é indefinida em e
Sendo assim, temos três candidatos à pontos críticos. vamos verificar se qual a mudança de sinal nas proximidades deles.
Perceba que, para valores dentro do intervalo , assume valores positivos (cresce). E para valores dentro do intervalo , irá assumir valores negativos (decresce). Logo, é um ponto de máximo no intervalo de
Já, para valores dentro do intervalo 1,2, assume valores negativos (decresce). E para valores dentro do intervalo , irá assumir valores negativos (decresce). Logo, não é um ponto de mínimo, nem máximo no intervalo de
Além disso, no intervalo assume valores positivos (cresce). E para valores dentro do intervalo , assume valores positivos (cresce). Logo, não é um ponto de mínimo, nem máximo no intervalo de
Resposta