Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.3 - Ex. 79
Uma família de curvas tem equações polares
Investigue como o gráfico muda quando varia. Em particular, você deveria identificar, plotando a curva com uma ferramenta gráfica, os valores de transição de para os quais o formato básico da curva muda.
Passo 1
Vamos começar fazendo . Nesse caso, temos
Que nada mais é do que uma circunferência de raio centrada na origem.
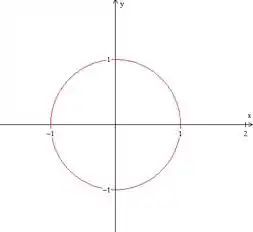
Passo 2
Agora vamos fazer variar, sendo .
- :
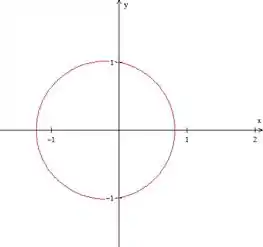
E percebemos que o gráfico deu uma andadinha para a esquerda.
- :
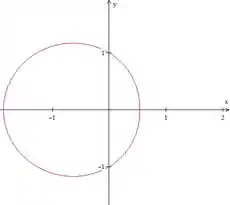
Aconteceu que, além de andar mais ainda para a esquerda, o gráfico ainda deu uma achatadinha no lado direito.
- :
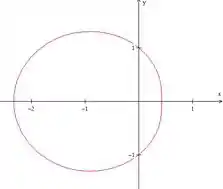
Parece que surge um biquinho beeeeeeeem sutil alí do lado direito.
- :
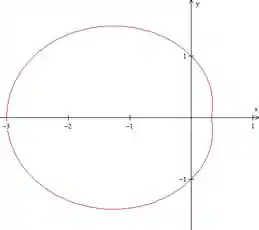
Já da pra ver um pouquinho melhor. É tipo uma ondulação na verdade.
Vamos aumentar um pouco mais o .
- :
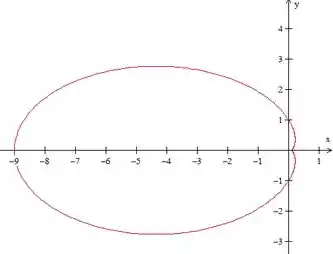
Aí sim!! Se aumentarmos um pouco mais..
- :
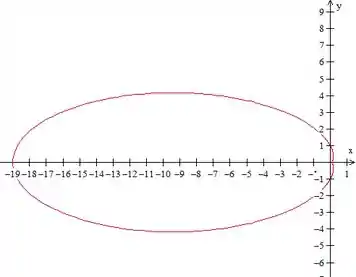
O que tá acontecendo é que a curva está se achatando horizontalmente, enquanto se desloca para a esquerda e o lado direito dela está fazendo um bico que está ficando cada vez mais pronunciado. Isto tudo enquanto .
Quando eis que:
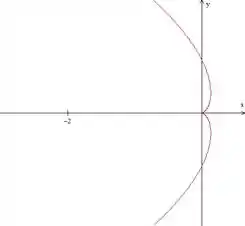
O bico se pronuncia de vez e a curva se achata tanto que a escala do printscreen nem seria capaz de pegar.
Passo 3
Agora o que acontece quando ?
-
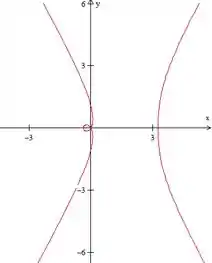
A curva agora se divide em duas partes e o lado esquerdo tem um looping.
- :
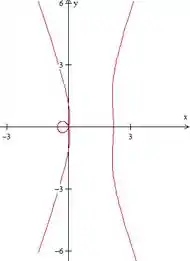
O looping da parte esquerda ficou maiorzinho e a parte direita ficou mais verticalizada, ao mesmo tempo que sua ponta esquerda fez um biquinho bem sutil. Pra confirmar isso, vamos aumentar um pouco o .
- :
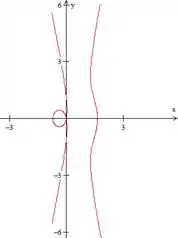
Viu só o biquinho? Agora a gente até consegue ver que tá mais pra uma ondulação né?
Passo 4
E se , o que que acontece?
Bom, nossa curva é
Se , temos
O que significa que teremos o mesmo comportamento que observamos aqui, só que com uma rotação de .
Resposta
Ei, a resposta está no passo a passo :)