Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.3 - Ex. 11
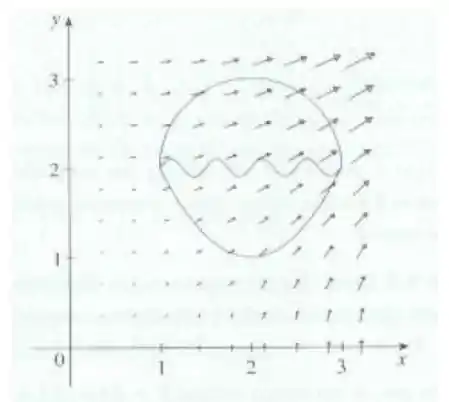
A figura abaixo mostra o campo vetorial e três curvas que começam em e terminam em .
- Explique por que tem o mesmo valor para as três curvas.
- Qual é esse valor comum?
Passo 1
Oi galera, tudo bem? Pra mostrar que aquela integral independe do caminho precisamos saber se o campo vetorial é conservativo.
Mas como? Calma que eu explico!
Um campo conservativo é aquele no qual as derivadas mistas das componentes são iguais, saca só. Se é:
Então para ser conservativo tem que satisfazer isso aqui:
Ok? Vamos aplicar para o campo dado? Bora lá:
E também:
Beleza! Esse campo vetorial é conservativo! Vamos agora determinar a função potencial associada a ele!
E temos que o valor da integral de caminho vai depender apenas da função potencial aplicada nos pontos final e inicial.
Passo 2
Vamos primeiro pegar uma das parciais, por exemplo e integrar em relação à :
Isso vai nos dar a função potencial mais uma constante só de , digamos (pois derivando em relação à ela desaparece, sacou?):
Pronto! Essa é a função potencial!
Tá, mas e aquela função de ali? Calma, no próximo passo vamos determinar ela!
Passo 3
Legal! O próximo passo é derivar a função potencial determinada em relação à :
Ta, mas e agora? Agora olha o pulo do gato! Vamos resgatar do passo a componente do campo dado:
E agora vamos igualar os dois lados!
Beleza! Agora integrando em relação à determinamos a função
Onde é uma constante qualquer.
Agora sim! Juntando com o resultado do passo temos a função potencial completa:
Passo 4
Show! Agora temos que o ponto final é e a função potencial nesse ponto é:
E no ponto inicial, que é a função vale:
Beleza! Agora sabemos que para um campo conservativo:
É isso! O valor em comum é !