Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.1 - Ex. 75
Quando um objeto estranho se aloja na traqueia, forçando uma pessoa a tossir, o diafragma empurra-o para cima, causando um aumento na pressão nos pulmões. Isso é acompanhado por uma contração na traqueia, fazendo um canal mais estreito por onde o ar expelido escoe. Para uma dada quantidade de ar escapar em um tempo fixo, é preciso que ele se mova mais rápido através do tubo mais estreito do que no mais largo. Quanto maior for a velocidade da corrente de ar, maior a força sobre o objeto estranho. O uso de raios X mostra que o raio do tubo circular da traqueia se contrai para cerca de 2/3 de seu raio normal durante a tosse. De acordo com o modelo matemático para a tosse, a velocidade está relacionada ao raio da traqueia pela equação.
Em que é uma constante e o raio normal da traqueia. A restrição sobre deve-se ao fato de que as paredes da traqueia endurecem sob pressão, evitando uma contração maior que (de outra forma, a pessoa ficaria sufocada).
- Determine o valor de no intervalo no qual tenha um máximo absoluto. Como isso se compara com a evidência experimental?
- Qual é o valor máximo absoluto de no intervalo?
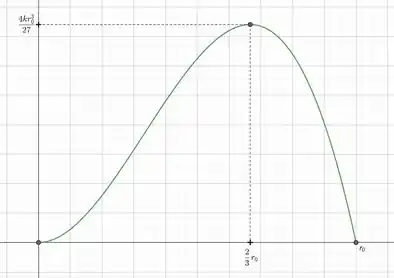
- Esboce o gráfico de no intervalo .
Passo 1
Olá, meu nobre e querido amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.
Nessa questão temos a função velocidade da traqueia de uma pessoa que é dada por:
Daí temos que encontrar nesse intervalo qual o valor do máximo absoluto. Para isso vamos derivar e igualar a zero e encontrar os pontos críticos.
E então usando o teorema do intervalo fechado, pois a função é contínua e definida dentro de um intervalo, vamos comparar a função no ponto crítico e nos extremos do intervalo e ver aonde que ela é máxima.
Sendo que a letra temos que encontrar o do máximo absoluto e na letra temos que encontrar o do máximo absoluto.Por fim, vamos esboçar o gráfico dessa função e para isso eu vou usar um software gráfico.
Passo 2
Para encontrar o máximo absoluto, nós derivamos a função e igualamos a zero, então
Nossa função é:
Fazendo a multiplicação
Derivando aplicando a regra da potência, temos:
Igualando a zero, temos:
Porém, note que e não está no intervalo dado, então, este valor não deve ser considerado
Também temos que:
Para continuarmos deveremos aplicar o método do invervalo fechado:
O Método do Intervalo Fechado - Para encontrar os valores máximo e mínimo absolutos de uma função contínua f em um intervalo fechado [a,b]:
1- Encontre os valores de f nos extremos do intervalo.
2- Encontre os valores de f nos números críticos de f em [a,b].
3- O maior valor das etapas 1 e 2 é o valor máximo absoluto, ao passo que o menor desses valores é o valor mínimo absoluto.
Agora, aplicando o método do intervalo fechado, necessitamos calcular e .
Substituindo os valores na equação da velocidade, :
Então, podemos concluir que é máximo quando e o valor exato de coincide com as evidências experimentais.
Passo 3
Pela parte (a), temos que máximo vai ser o valor de em
Passo 4
Esboçando o gráfico, ficamos com
