Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 4.6 - Ex. 11
Obtenha os gráficos de que revelem todos os aspectos importantes da curva. Estime os intervalos de crescimento e decrescimento, valores extremos, intervalos de concavidade e pontos de inflexão, e use o calculo para achar essas quantidades exatamente.
Passo 1
Oi oi, bora para mais uma?
Nessa questão temos a seguinte função:
E a partir dos gráficos de , e estimar os intervalos de crescimento, decrescimento, valores extremos, intervalos de concavidade e pontos de inflexão.
O gráfico da derivada , nos indica o crescimento da função de forma que:
Indica que a cresce e
Indica que a decresce.
indica que a função pode ter um valor extremo de forma que se a função crescia e depois decresce, esse ponto representa um máximo e se a função decrescia e depois cresce, esse ponto representa um mínimo.
O gráfico da segunda derivada , nos indica a concavidade da função de forma que:
Indica que a tem concavidade para cima e
Indica que a tem concavidade para baixo.
indica que a função possui um ponto de inflexão desde que nesse ponto a segunda derivada troque de sinal.
Para fazer essa questão vamos encontrar a derivada primeira e segunda dessa função e então plotar esses gráficos.
Passo 2
Nossa função é:
Seu gráfico é o seguinte:
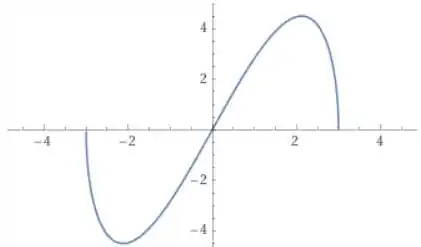
Repare que essa função só é definida entre . Isso ocorre pois temos uma raíz que não pode ter um valor negativo no seu interior.
Fazendo a derivada primeira, aqui temos uma regra do produto além da regra da cadeia para resolver a derivada de .
Seu gráfico é:
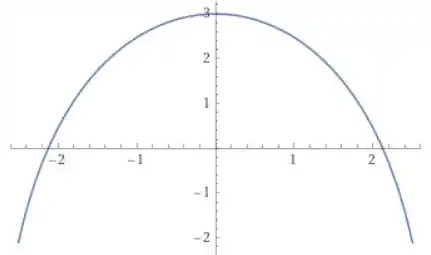
Fazendo agora a derivada segunda:
Vamos usar aqui a regra do quociente, além da regra do cadeia.
Fazendo a soma de frações no numerador, temos:
De forma que temos no final das contas:
E o gráfico de é portanto:
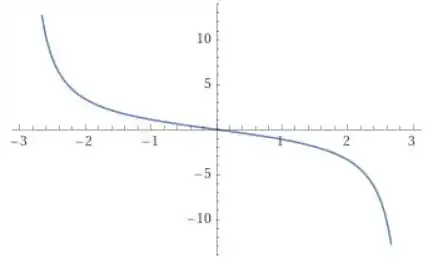
Passo 3
Fazendo as estimativas, temos que:
quando e portanto a função é decrescente nesse intervalo. quando e portanto a função é crescente nesse intervalo. quando e portanto a função é decrescente nesse intervalo.
Dessa forma temos que é um ponto de mínimo absoluo e é um ponto de máximo absoluto.
Com relação a segunda derivada temos que:
quando , logo a função tem concavidade para cima nesse intervalo.
quando , logo a função tem concavidade para baixo nesse intervalo.
Dessa forma, é um ponto de inflexão.
Resposta
quando e portanto a função é decrescente nesse intervalo. quando e portanto a função é crescente nesse intervalo. quando e portanto a função é decrescente nesse intervalo.
Dessa forma temos que é um ponto de mínimo absoluo e é um ponto de máximo absoluto.
Com relação a segunda derivada temos que:
quando , logo a função tem concavidade para cima nesse intervalo.
quando , logo a função tem concavidade para baixo nesse intervalo.
Dessa forma, é um ponto de inflexão.