Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.3 - Ex. 82

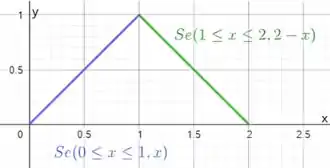
Considere

f x = 0 ,     s e   x < 0 x ,     s e   0 ≤ x ≤ 1 2 - x ,     s e   1 < x ≤ 2 0 ,     s e   x > 2

E

g x = ∫ 0 x f t d t

  1. Ache uma expressão para g ( x ) similar àquela para f ( x )
  2. Esboce os gráficos de f e g
  3. Onde f é derivável? Onde g é derivável?

Passo 1

Eaeee, belezinha? Bom... a questão nos dá uma função f x dada da seguinte forma:

f x = 0 ,     s e   x < 0 x ,     s e   0 ≤ x ≤ 1 2 - x ,     s e   1 < x ≤ 2 0 ,     s e   x > 2

E nos diz que g x é uma função dada da seguinte forma:

g x = ∫ 0 x f t d t

Com isso, a questão nos pede para encontrar uma expressão para g x da mesma forma que f x , ou seja, com aqueles intervalos dados.

Para isso, temos que calcular a integral de f x para cada intervalo dado, ou seja, teremos que fazer 4 integrais diferentes, mas com muita atenção nos limites de integração.

Ademais, a questão também nos pede para esboçar os dois gráficos e dizer onde cada função é derivável, ou seja, aqui deveremos verificar se há descontinuidade.

Muita coisa, né? Então vamos devagarinho que vai dar certo!! 😉

Passo 2

Vamos fazer a letra a) resolvendo a integral para cada intervalo de f x a fim de encontrarmos g x , ou seja, integrar cada função para o seu limite de integração:

  • 0 ; se x < 0 temos que:

Neste caso, f ( t ) = 0 em todo o intervalo de integração (de 0 a x ), então a integral é simplesmente

g x = ∫ 0 x f t d t

g 1 x = ∫ 0 x 0 d t → g 1 x = 0

  • x ; se 0 ≤ x ≤ 1 temos que:

    • Novamente temos uma função que é constante em todo o intervalo, notamos isso por essa notação de menor e igual:   s e   0 ≤ x ≤ 1

    g x = ∫ 0 x f t   d t

    g 2 x = ∫ 0 x t   d t →   g x = t 2 2 0 x

    g 2 x = x 2 2

  • 2 - x ; se 1 < x ≤ 2 temos que:

    • Aqui temos um intervalo em qual a função não é constante, note que ela não engloba x = 1 , apenas x > 1 , por isso que separamos os intervalos de integração, pois para x ≤ 1 , temos outro intervalo definido, aqui usaremos o que já calculamos acima:

    g x = ∫ 0 x f t d t

    A aqui aplicamos os intervalos que discutimos:

    g 3 x = ∫ 0 1 f t d t + ∫ 1 x f t d t

    E note a a função que colocamos na integral é a função correspondente aquele domínio!

      g 3 x = ∫ 0 1 t   d t + ∫ 1 x 2 - t d t

    g 3 x = 1 2 x 2 0 1 + 2 t - t 2 2 1 x

    Analisando para os intervalos:

    g 3 x = 1 2 1 2 - 1 2 0 2 + 2 x + x 2 x - 2 - 1 2

    g 3 x = 2 x - x 2 2 - 1

  • 0 ,   se x > 2 :

Para x > 2 , a função f ( t ) muda de expressão em t = 1 e t = 2 , então precisamos dividir a integral em três partes: uma de 0 a 1 (onde f ( t ) = t ), outra de 1 a 2 (onde f ( t ) = 2 - t ), e a última de 2 a x (onde f ( t ) = 0 ):

g x = ∫ 0 x f t d t

Repare nos intervalos e nas funções dentro das integrais, cada domínio com sua função correspondente:

g 4 x = ∫ 0 1 t d t + ∫ 1 2 2 - t d t + ∫ 2 x 0 d t

g 4 x = 1 2 x 2 0 1 + 2 x - x 2 2 1 2 + 0

Agora substituindo os valores:

g 4 x = 1 2 1 2 - 1 2 0 2 + 2 ⋅ 2 - 2 2 2 - 2 ⋅ 1 - 1 2 2 + 0 = 1

Então, podemos escrever g ( x ) como

g x = 0 ,     s e   x < 0 x 2 2 ,     s e   0 ≤ x ≤ 1 2 x - x 2 2 - 1 ,     s e   1 < x ≤ 2 1 ,     s e   x > 2

Passo 3

Para esboçar os gráficos, a gente só tem que olhar para os intervalos 0 ≤ x ≤ 1 e 1 ≤ x ≤ 2 , pois o resto é zerado.

Assim, fazendo f x , temos o seguinte esboço:

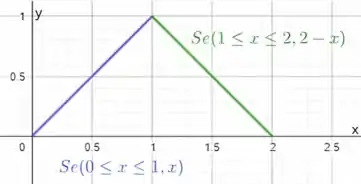
E, para g x , de forma análoga, temos o seguinte esboço:

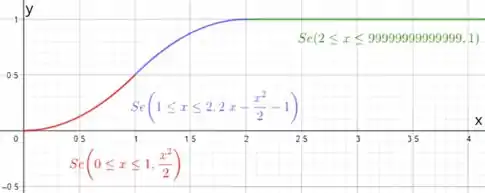
Passo 4

A função f não é diferenciável nos “bicos”, então f não é diferenciável nos pontos x = 0 ,   1   e   2 . Observe no gráfico f ( x ) .

Assim, f   é diferenciável nos intervalos:

- ∞ , 0 ,   0,1 ,   1,2   e   2 , ∞

A função g é diferenciável em todo seu domínio, ou seja, no intervalo, repare como o gráfico de g ( x ) é suave.

- ∞ , ∞

Resposta

  1. g x = 0 ,     s e   x < 0 x 2 2 ,     s e   0 ≤ x ≤ 1 2 x - x 2 2 - 1 ,     s e   1 < x ≤ 2 1 ,     s e   x > 2

(c) f   é diferenciável no intervalo

- ∞ , 0 ,   0,1 ,   1,2   e   2 , ∞

A função g é diferenciável em todo seu domínio, ou seja, no intervalo

- ∞ , ∞

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se int_(- 2)^2 3 f ( x ) d x = 12 , int_(- 2)^5 f ( x ) d x = 6 , int_(- 2)^5 g ( x ) d x = 2 , determine int_(- 2)^2 f ( x ) d x
Se int_(- 2)^2 3 f ( x ) d x = 12 , int_(- 2)^5 f ( x ) d x = 6 , int_(- 2)^5 g ( x ) d x = 2 , determine int_5^(- 2) g ( x ) d x
Se int_0^2 f ( x ) d x = pi , int_0^2 7 g ( x ) d x = 7 , int_0^1 g ( x ) d x = 2 , determine int_0^2 g ( x ) d x
Expresse o limite com uma integral definida . Depois, calcule a integral para determinar o valor do limite. P é uma partição do intervalo dado e os números c k são escolhidos dentro dos subintervalos
Se int_0^2 f ( x ) d x = pi , int_0^2 7 g ( x ) d x = 7 , int_0^1 g ( x ) d x = 2 , determine int_0^2 g ( x ) d x