Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.5 - Ex. 65

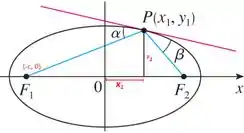
Seja P x 1 , y 1 um ponto na elipse x 2 a 2 + y 2 b 2 = 1 com focos F 1 e F 2 e seja α e β os ângulos entre as retas P F 1 , P F 2 e a elipse, como na figura. Demonstre que α = β . Isso explica como galerias de sussurros e litotripsia funcionam. O som vindo de um dos focos é refletido e passa pelo outro foco. [Sugestão: Use a fórmula no Problema 17 na página 250 , no Volume I para mostrar que t g   α = t g   β .]

Passo 1

Bom, galera. Nesse problema a gente tem uma elipse, e queremos provar que existe uma propriedade legal sobre alguns ângulos.

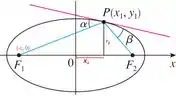
Quando ele fala “ângulo entre a reta P F 1 e a elipse”, ele quer dizer o ângulo entre a reta que passa pelos pontos P e F 1 e a reta tangente à elipse, cuja inclinação é a derivada nesse ponto P .

Então nós temos que mostrar que esse e o ângulo entre a reta P F 2 e a elipse, ou seja, α e β , representados na figura, são iguais, beleza?

Vamos seguir os passos

  1. Através da imagem iremos calcular a inclinação das retas nos pontos P F 1 ( m 2 ) e P F 2 ( m 1 .
  2. Utilizar a equação da reta tangente para obter os ângulos

t g   α = m 1 - m 1 + m 1 m

Agora é só calcular!

Passo 2

Pra mostrar que os ângulos são iguais, teremos que mostrar que suas tangentes s��o iguais, seguindo a sugestão do enunciado. Então vamos trabalhar com as inclinações das retas, certo?

Seja m a inclinação da reta tangente à elipse no ponto P (derivada), m 1 a inclinação da reta P F 1 e m 2 a inclinação da reta P F 2 . Olhando a figura, veja que:

m 1 = y 1 - 0 x 1 - - c = y 1 x 1 + c

m 2 = y 1 x 1 - c  

Agora, pra calcular m , vamos derivar a equação da elipse. Não se esqueça da regra da cadeia pra derivar termos envolvendo y , ok?

x 2 a 2 + y 2 b 2 = 1

1 a 2   2 x + 1 b 2   2 y   d y d x = 0

2 y b 2   d y d x = - 2 x a 2

d y d x = - b 2 x a 2 y

Para o ponto P , temos:

m = - b 2 x 1 a 2 y 1

Passo 3

Agora que temos as inclinações de cada reta, podemos usar a fórmula pra calcular a tangente do ângulo entre duas retas.

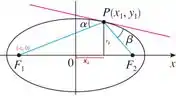
Como α é o ângulo entre a reta P F 1 e a reta tangente à elipse, temos:

t g   α = m 1 - m 1 + m 1 m

t g   α = y 1 x 1 + c - - b 2 x 1 a 2 y 1 1 + y 1 x 1 + c - b 2 x 1 a 2 y 1

t g   α = a 2 y 1 2 + b 2 x 1 x 1 + c a 2 y 1 x 1 + c - b 2 x 1 y 1

t g   α = a 2 y 1 2 + b 2 x 1 2 + b 2 c x 1 ( a 2 - b 2 ) x 1 y 1 + a 2 c y 1

Pela equação da elipse, temos:

a 2 y 1 2 + b 2 x 1 2 = a 2 b 2         e         a 2 - b 2 = c 2

t g   α = a 2 b 2 + b 2 c x 1 c 2 x 1 y 1 + a 2 c y 1

t g   α = b 2 a 2 + c x 1 c y 1 c x 1 + a 2

t g   α = b 2 c y 1

Passo 4

Agora fazemos os cálculos para β , que é o ângulo entre a reta P F 2 e a reta tangente à elipse:

t g   β = m 2 - m 1 + m 2 m

t g   β = y 1 x 1 - c - - b 2 x 1 a 2 y 1 1 + y 1 x 1 - c - b 2 x 1 a 2 y 1

Realizando o MMC no numerador e no denominador

t g   β = y 1 ² a 2 + b 2 x 1 ( x 1 - c ) ( x 1 - c ) a 2 y 1 a 2 y 1 ( x 1 - c ) + y 1 ² a 2 - b 2 x 1 ( x 1 - c ) ( x 1 - c ) a 2 y 1

Aplicando a propriedade de divisão de frações, repetimos a primeira fração e multiplicamos pela inverso da segunda fração.

t g   β = a 2 y 1 2 + b 2 x 1 x 1 - c a 2 y 1 x 1 - c - b 2 x 1 y 1

Multiplicação distribuitiva

t g   β = a 2 y 1 2 + b 2 x 1 2 - b 2 c x 1 a 2 - b 2 x 1 y 1 - a 2 c y 1

t g   β = a 2 b 2 + b 2 c x 1 c 2 x 1 y 1 + a 2 c y 1

Podemos colocar termos em evidência

t g   β = b 2 a 2 + c x 1 c y 1 c x 1 + a 2

t g   β = b 2 c y 1

Então concluímos que t g   α = t g   β ,   e portanto, α = β .

Resposta

Demostração

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule a inclinação da reta tangente para a curva polar dada no ponto especificado pelo valor de θ . r = 2 sen ⁡ θ ,θ = π / 6
Calcule a inclinação da reta tangente para a curva polar dada no ponto especificado pelo valor de θ . r = cos ⁡ ( θ / 3 ) ,θ = π
Calcule a inclinação da reta tangente para a curva polar dada no ponto especificado pelo valor de θ . r = cos ⁡ ( 2 θ ) ,θ = π / 4
Calcule a inclinação da reta tangente para a curva polar dada no ponto especificado pelo valor de θ . r = 2 - sen ⁡ θ ,θ = π / 3
Encontre os pontos na curva dada onde a reta tangente é horizontal ou vertical. r 2 = sen ⁡ 2 θ