Enunciado
Cálculo - Guidorizzi - Vol 3- Ed: 5º - Capítulo 11.1 - Ex. 14-a
14. Seja r > 0 um real dado e considere a superfície
com (φ, θ) ∈ K, onde K é o retângulo e 0 ≤ θ ≤ 2π, no planoφθ. (Observe que a imagem de σ é a semissuperfície esférica
Seja γ a fronteira de K orientada no sentido anti-horário. Seja Γ1 dada pora) Desenhe a imagem de Γ1.
Passo 1
Estamos trabalhando com a superfície abaixo
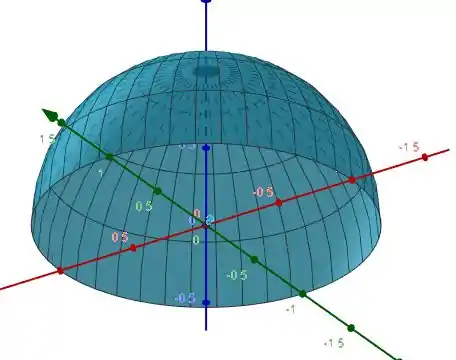
Onde é a cúpula e é a borda dessa cúpula formada por
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Uma partícula se move ao longo dos segmentos de reta da origem para os pontos 1,0 , 0 , 1,2 , 1 , ( 0,2 , 1 ) e de volta a origem sob a influência do campo de força F x , y , z = z 2 i + 2 x y j + 4 y
Use o Teorema de Stokes para calcular ∫ C F . d r . Em cada caso, C é orientada no sentido anti-horário como visto acima. F x , y , z = 2 y i + ( x z ) j + ( x + y ) k C é a curva resultante da inters
Use o Teorema de Stokes para calcular ∫ C F . d r , onde F x , y , z = x 2 z i + x y 2 j + z 2 k e C é a curva resultante do plano x + y + z = 1 e o cilindro x 2 + y 2 = 9 , orientado no sentido anti-
Verifique se o Teorema de Stokes é verdadeiro para o campo vetorial F e superfície S . F x , y , z = - 2 y z i + y j + 3 x k S é parte do paraboloide z = 5 - x 2 - y 2 que está acima do plano z = 1 ,
Verifique que o Teorema de Stokes é verdadeiro para o campo vetorial dado F → e a superfície S . F → x , y , z = - 2 y z i ^ + y j ^ + 3 x k ^ , S é a parte do paraboloide z = 5 - x 2 - y 2 que está a