Enunciado
Cálculo - Dennis G. Zill - Equações Diferenciais - Vol 1- Ed: 3º - Capítulo 3.2 - Ex. 30
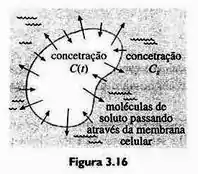
Suponha uma célula suspensa em uma solução contendo um solvente de concentração constante . Suponha ainda que a célula tenha volume constante e que a área de sua superfície permeável também seja constante igual a . Pela lei de Fick, a taxa de variação de sua massa é diretamente proporcional à área e á diferença , em que é a concentração do solvente dentro da célula no instante . Encontre se e . Veja a Figura 3.16.
Passo 1
Então pessoal, de início precisamos estabelecer uma equação diferencial que descreva nosso problema, ok? A questão nos diz que a taxa de variação da massa é DIRETAMENTE proporcional à área e a diferença , logo teremos:
Como devemos ter uma constante de proporcionalidade:
Além disso, o enunciado nos diz que , então substituindo teremos:
Opa! Encontramos nossa equação diferencial! Então bora que bora resolver isso aí!
Passo 2
A nossa equação diferencial pode ser resolvida pelo método de separação de variáveis, saca só:
Integrando ambos os lados:
O que nos dá como resultado:
Logo:
Show!
Passo 3
O enunciado também nos dá uma condição inicial para determinarmos . A condição dada foi . Aplicando, teremos:
Substituindo na nossa solução geral:
E esse é nosso resultado, galera! 😉