Enunciado
Cálculo - Um curso de Cálculo Volume 2 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 16.4 - Ex. 3
Suponha que represente a distribuição da temperatura no plano. Seja
Passo 1
Vamos calcular as derivadas parciais,
Encontrando os números críticos,
é ponto crítico. Aplicando
Passo 2
Vejamos fronteira,
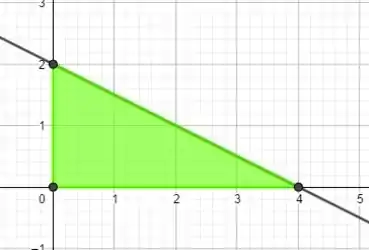
Temos que são os ppntos de fronteira, aplicando
Resposta
é minimo.
Exercícios de Livros Relacionados
Nos Exercícios 31-38, encontre os máximos e mínimos absolutos das funções nos domínios dados. f x ,y = 4 x - 8 x y + 2 y + 1 na placa triangular limitada pelas retas x = 0 , y = 0 , x + y = 1 no prime
Nos Exercícios 31-38, encontre os máximos e mínimos absolutos das funções nos domínios dados. f x ,y = 4 x - x 2 cos y na placa retangular 1 ≤ x ≤ 3 , - π / 4 ≤ y ≤ π / 4 (veja a figura a seguir).
Nos Exercícios 31-38, encontre os máximos e mínimos absolutos das funções nos domínios dados. D x ,y = x 2 - x y + y 2 + 1 na placa triangular fechada e limitada pelas retas x = 0 , y = 4 , y = x no p
Nos Exercícios 31-38, encontre os máximos e mínimos absolutos das funções nos domínios dados. f x ,y = 48 x y - 32 x 3 - 24 y 2 na placa retangular 0 ≤ x ≤ 1 , 0 ≤ y ≤ 1 .
Nos Exercícios 31-38, encontre os máximos e mínimos absolutos das funções nos domínios dados. f x ,y = x 2 + y 2 na placa triangular fechada e limitada pelas retas x = 0 , y = 0 , y + 2 x = 2 no prime