Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 6.2 - Ex. 35
Use um gráfico para encontrar coordenadas aproximadas dos pontos de interseção das curvas fornecidas. Em seguida, use sua calculadora para encontrar (aproximadamente) o volume do sólido obtido girando sobre o eixo a região delimitada por essas curvas.
Passo 1
Seguindo as instruções do enunciado vamos plotar ambas as funções em um mesmo gráfico a fim de encontrarmos o ponto de interseção entre as curvas. Então, teremos
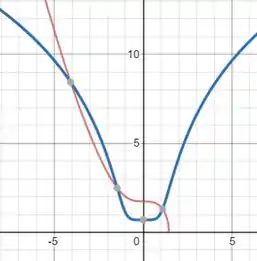
A primeira coisa que reparamos é que em um determinado intervalo temos uma função por cima e em outro momento a outra função está por cima, então, para acharmos o volume desejado deveremos separar em duas integrais dadas por
Aproximaremos os valores de por
Então, nosso volume fica sendo
Resposta
Exercícios de Livros Relacionados
27. A região limitada pela curva y = c o t gx , pela reta x = π 6 , e pelo eixo x é girada em torno do eixo x . Ache o volume do sólido gerado.
18. Deduza a fórmula para o volume de um cone circular reto com h unidades de altura e a unidades de raio da base, rotacionando a região limitada pelo triângulo retângulo em torno de um de seus cateto
29. Ache o volume do sólido gerado pela rotação, em torno da reta x = - 4 , da região limitada por aquela reta e pela parábola x = 4 + 6 y - 2 y 2 .
30. Ache o volume do sólido gerado pela rotação, em torno do eixo x , da região limitada pela parábola y 2 = 4 x e pela reta y = x .
25. Ache o volume do sólido gerado se a região do Exercício 23 girar em torno da reta y = 1 .