Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.5 - Ex. 27
Use o roteiro dessa seção para esboçar a curva:
Passo 1
Oii pessoal, show de bola??
“A loucura é como a gravidade, só precisa de um empurrãozinhooo...”
Bora empurrar e macetar essa questãozinha comigo agora
A questão pede para esboçar a curva da função dada:
Para isso, precisamos entender como essa função se comporta ao longo do domínio permitido de
Para esboçar a curva de uma função, geralmente seguimos esses passos:
Encontrar o domínio da função.
Analisar o comportamento da função nos pontos críticos (zeros, assíntotas, etc.).
Calcular derivadas para encontrar máximos, mínimos e pontos de inflexão.
Plotar alguns pontos para ter uma ideia do comportamento da função.
Desenhar o gráfico com base nas análises anteriores.
Passo 2
A função dada é:
Vamos seguir os passos detalhados acima.
Encontrar o domínio da função:
Para que seja real, o radicando deve ser maior ou igual a zero:
Além disso, não pode ser zero porque está no denominador:
Portanto, o domínio da função é:
Passo 3
- Para ou , o denominador tende a zero, fazendo com que a função tende ao infinito positivo ou negativo, respectivamente.
- Nos extremos do domínio, ou seja, o numerador será zero, logo
Para encontrar os pontos críticos, derivamos
Usamos a regra do quociente:
Onde:
Passo 4
Logo:
Não há zeros na derivada, então não há máximos ou mínimos locais.
Passo 5
Vamos calcular alguns pontos para visualizar o gráfico:
- Para
- Para
Passo 6
No gráfico gerado, podemos observar o comportamento da função
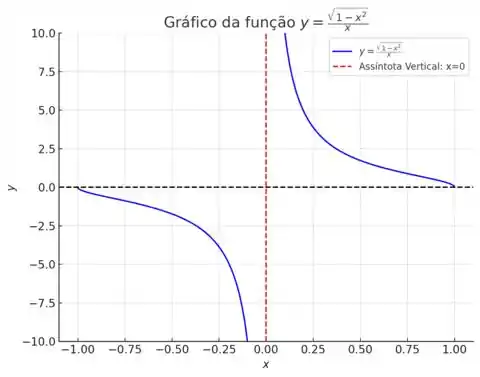
- Assíntota vertical em À medida que se aproxima de zero, os valores de tendem ao infinito positivo e ao infinito .
Isso é indicado pela linha vermelha pontilhada no gráfico.
- Interceptação do eixo Nos pontos a função toca o eixo onde
Esses são os pontos onde o numerador da função é zero.
- Comportamento da curva: Para valores de entre (excluindo zero), a curva apresenta simetria em relação ao eixo mas com valores negativos de à esquerda de e valores positivos de à direita de
O gráfico mostra claramente que a função tem um comportamento divergente perto de
, com uma assíntota vertical, e cruza o eixo nos pontos
“Faça seus medos terem medo de você”
Resposta
Vide o passo a passo.