Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 15.4 - Ex. 20

Utilize a integral dupla para determinar a área da região.

20- A região dentro do círculo r = 4   s e n   θ e fora do círculo r = 2

Passo 1

Fala ai pessoal, o exercício nos pede para utilizar a integral dupla para determinar a área região dentro do círculo r = 4   s e n   θ e fora do círculo r = 2 .

Vou desenhar o gráfico para ficar mais fácil de visualizar, mas não precisamos dele para resolver essa questão.

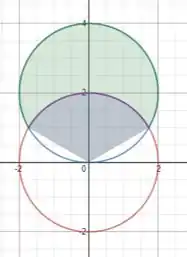
A primeira coisa que iremos fazer para montarmos a integral será escolher algum tipo de coordenada, como se trata de um círculo a melhor opção é utilizar as coordenadas polares. Logo a nossa integral vai ter a seguinte cara :

A = ∫ θ 1 θ 2 ∫ r 1 ( θ ) r 2 ( θ ) r   d r   d θ

Show, o próximo passo é achar os limites de integração para r e θ e aí sim podemos resolver a integral .

Vamos lá !

Passo 2

Bom , nós já sabemos que vamos utilizar as coordenadas polares , e que ela terá o formato :

A = ∫ θ 1 θ 2 ∫ r 1 ( θ ) r 2 ( θ ) r   d r   d θ

Agora precisamos achar os limites de integração.

Vamos começar por r . O enunciado nos informa que :

r = 4   s e n   θ  

e

  r = 2

Logo podemos dizer que : 2   ≤ r ≤ 4   s e n   θ  

Mas vamos lembrar que o enunciado nos deu dois círculos , onde a região está dentro do círculo de de r = 4   s e n   θ   e fora de   r = 2 .

Dessa forma vamos precisar achar a interseção entre essas duas curvas para saber o limite que a região que queremos irá ter , para isso, basta igualar as funções.

2 = 4   s e n   θ

s e n   θ = 2 4

s e n   θ = 1 4

Sendo assim, os valores de θ serão :

θ = π 6   e 5 π 6

Vamos montar nossa integral :

A = ∫ π 6 5 π 6 ∫ 2 4   s e n   θ r   d r   d θ

Passo 3

Agora podemos começar os cálculos :

A = ∫ π 6 5 π 6 ∫ 2 4   s e n   θ r   d r   d θ

Começamos resolvendo a primeira integral , fazemos sempre pela ordem dos diferenciais:

∫ 2 4   s e n   θ r   d r

1 2 r 2 2 4   s e n   θ

1 2 ( 4   s e n θ )   2 -   2 2

∫ 2 4   s e n   θ r   d r =   1 2 16   s e n 2 θ - 4

Vamos substituir na integral :

A = ∫ π 6 5 π 6 ∫ 2 4   s e n   θ r   d r   d θ

⇓

A = ∫ π 6 5 π 6   1 2 16 s e n 2 θ - 4   d θ

Passo 4

Beleza, agora podemos resolver a segunda integral :

∫ π 6 5 π 6   1 2 16 s e n 2 θ - 4   d θ

Vamos fazer a distributiva de 1 2 :

∫ π / 6 5 π / 6 8 s e n 2 θ - 2 d θ

Pelas relações trigonométricas abaixo temos:

s e n 2 θ + c o s   2 θ = 1  

e

  c o s 2 θ = c o s ( 2 θ )   - 1 2    

Assim podemos dizer que :

s e n 2   θ = 1 - c o s   2 θ   2

Dessa forma temos , substituindo s e n 2   θ :

∫ π / 6 5 π / 6 8 s e n 2 θ - 2 d θ

⇩

∫ π / 6 5 π / 6 8 1 - c o s   2 θ   2 - 2 d θ

Simplificando :

A = ∫ π 6 5 π 6 ( 4 ( 1 - c o s   2 θ ) - 2 ) d θ  

Fazendo a distributiva:

A = ∫ π 6 5 π 6 ( ( 4 - 4   c o s   2 θ ) - 2 ) d θ  

A = ∫ π 6 5 π 6 ( 2 - 4 c o s   2 θ )   d θ  

Passo 5

Podemos dividir em duas integrais para ficar mais fácil de visualizar :

A = ∫ π 6 5 π 6 2 d θ - ∫ π 6 5 π 6 4 c o s   2 θ   d θ  

Vamos resolver a primeira , mas aqui tanto faz a ordem de resolução :

∫ π 6 5 π 6 2 d θ

2 θ   π 6 5 π 6

2 . 5 π 6 - 2 π 6  

∫ π 6 5 π 6 2 d θ = 4 π 3

Vamos substituir em:

A = ∫ π 6 5 π 6 2 d θ - ∫ π 6 5 π 6 4 c o s   2 θ   d θ  

⇓

A = 4 π 3 - ∫ π 6 5 π 6 4 c o s   2 θ   d θ  

Passo 6

Agora vamos para segunda integral :

∫ π 6 5 π 6 4 c o s   2 θ   d θ

4 1 2 s i n   ( 2 θ )   π 6 5 π 6

4 1 2 s i n ( 2 . 5 π 6 ) - 1 2 s i n   ( 2 . π 6 )  

4 1 2 s i n   ( 5 π 3 ) - 1 2 s i n   ( π 3 )  

Colocando o meio para fora:

2 s i n   ( 5 π 3 ) - s i n   ( π 3 )  

∫ π 6 5 π 6 4 c o s   2 θ   d θ = 2 - 3

substituindo em :

A = 4 π 3 - ∫ π 6 5 π 6 4 c o s   2 θ   d θ  

⇓

A = 4 π 3 - 2 - 3  

Logo a área será:

A = 4 π 3 + 2 3

Resposta

A = 4 π 3 + 2 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um pulverizador agrícola distribui água em um padrão circular de 50m de raio. Ele fornece água até uma profundidade de e - r metros por hora a uma distância de r metros do pulverizador.(a) Se 0R ≤ 100
Uma piscina circular tem diâmetro de 10 metros. A profundidade é constante ao longo das retas de leste para oeste e cresce linearmente de 1 metro na extremidade sul para dois metros na extremidade nor
Uma região R é mostrada na figura. Decida se você deve usar coordenadas polares ou retangulares e escreva ∬ R f x , yd A como uma integral iterada, onde f é uma função qualquer contínua em R .
Uma região R é mostrada na figura. Decida se você deve usar coordenadas polares ou retangulares e escreva ∬ R f x , yd A como uma integral iterada, onde f é uma função qualquer contínua em R .
Calcule a integral dada, colocando-a em coordenadas polares. ∬ R 4 - x 2 - y 2d A , onde R = x , yx 2 + y 2 ≤ 4 ,x ≥ 0 } .