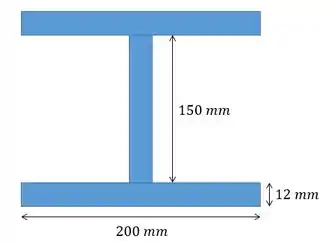
Uma coluna de aço tem comprimento de e está engastada na base e livre no topo. Se a área da seção transversal river as dimensões mostradas na figura, determine a carga crítica
Passo 1
Bom dia, pessoal!!!
Olhem só como essa questão foi boa com a gente rsrs...
Ela já falou que o aço será utilizado, logo e . Além disso forneceu o comprimento . Se a gente olhar nossa equação da carga crítica vamos ter:
Então falta só a gente calcular o momento de inércia e achar o valor de . Então partiu achar essas coisitchas.
Passo 2
Primeiro vamos achar o termo . Esse termo é definido unicamente pelas condições dos apoios e segue sempre o mesmo padrão, e a gente viu na teoria que para o caso engastado na base e livre no topo vamos ter :
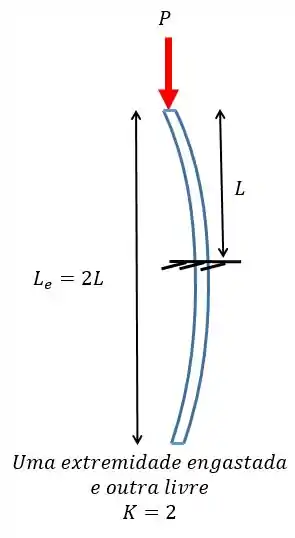
Pronto! Agora é só calcular o momento de inércia e partir pro abraço!
Passo 3
Pessoal, a flambagem sempre vai ocorrer no eixo de menor momento de inércia, correto? Correto! Isso tem que ter no sangue!!!
Como temos um perfil de abas largas é importante saber que o eixo de menor momento de inércia é o aquele que passa exatamente pela alma:
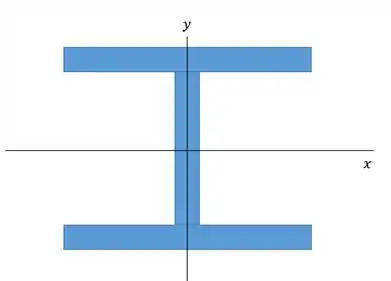
Então o nosso momento de inércia será calculado como a soma de cada uma das três barras, utilizando o eixo como a base:
Passo 4
Agora é só substituir na equação da força crítica:
Passo 5
Pessoal, a gente já até achou a carga crítica mas é importante também saber se não ultrapassamos o limite de escoamento do material também. Como o aço tem , então a gente vai fazer:
Calculando a área vamos ter:
Então vamos ter:
Como essa tensão é menor do que então a nossa coluna pode ser utilizada no projeto já que não irá flambar e nem escoar =D