Dois estudantes de engenharia, depois de tomar algumas cervejas, decidem entrar na faculdade e realizar um teste de flambagem utilizando uma máquina de compressão. Sabendo que os dois alunos utilizaram um corpo de prova de aço com de comprimento e de seção retangular com , sabendo também que eles posicioram o corpo de prova de forma que esteja engastado em ambos as extremidades, diga se eles conseguirão chegar ao ponto de flamgabem ou se o material irá escoar antes.
Passo 1
Que questão doida essa né? kkkk
Enfim, vamos ao que importa. A questão pede para avaliarmos o que acontece primeiro a flambagem ou o escoamento. Para isso a gente vai precisar calcular a tensão crítica de flambagem e comparar com a tensão de escoamento. Faz sentido não faz?
Só para lembrar que o problema deu a tensão de escoamento e a tensão crítica de flambagem pode ser encontrada através da seguinte equação:
Ou
obs: É a mesma equação. A única diferença é a consideração do raio de giração
Passo 2
Bom, partiu então resolver. Vamos calcular a tensão crítica de flambagem, para isso temos que calcular o momento de inércia e área.
Área:
O momento de inércia:
Como o momento de inércia deve ser o menor possível relativo à seção transversal vamos ter:
Só precisamos de mais uma coisinha antes de substituir na equação da tensão crítica, é saber qual o valor do fator de comprimento efetivo . Pela tabela nós vamos ter que para o caso de ambas as extremidades engastadas
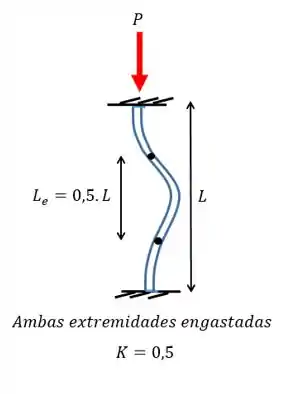
Passo 3
Agora sim é só substituir na equação:
Percebe que esse valor é bem superior ao valor da tensão máxima de escoamento
Logo, os nossos dois estudantes alcoolizados não conseguiram realizar o teste de flabagem, pois o corpo de prova falhou devido à compressão antes.
Passo 4
Percebe que esse valor é bem superior ao valor da tensão máxima de escoamento
Logo, os nossos dois estudantes alcoolizados não conseguiram realizar o teste de flabagem, pois o corpo de prova falhou devido à compressão antes.
Resposta
Ei, a resposta está no passo a passo :)