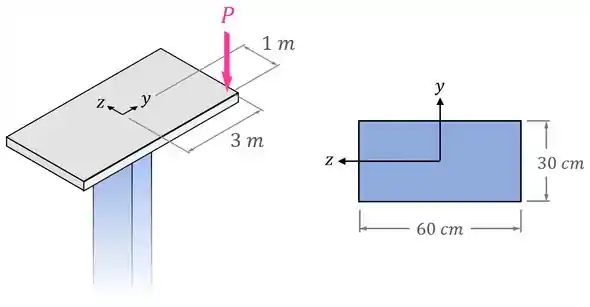
Uma força é aplicada na plataforma da figura abaixo, que é sustentada por uma coluna retangular (em azul na figura) com uma seção transversal de . A posição da força em relação ao centro da plataforma e da coluna está indicada na figura.
Determine a tensão normal máxima nessa coluna.
Passo 1
O que está acontecendo?
A carga excêntrica vai gerar, no centro da coluna:
- Um momento em relação ao eixo ;
- Um momento em relação ao eixo ;
- E uma força axial ,
Como mostra a figura abaixo:

Todos esses três carregamentos vão gerar tensões normais nessa coluna:
Primeiro, o momento em relação ao eixo vai gerar uma tensão normal de flexão de acordo com a fórmula da flexão de sempre:
Onde:
- é o momento em relação ao eixo , positivo no sentido que está desenhado na figura acima, que já é também o sentido do momento gerado pela força ;
- é a posição do ponto em que se quer avaliar a tensão em relação à linha neutra, localizada no eixo ;
- & é o momento de inércia da área da seção transversal dessa coluna em relação ao eixo .
Lembrando que pode ser calculado para um retângulo usando a fórmula:
Sendo que nesse caso, a base (que é paralela à linha neutra no eixo ) vai ser e a altura (perpendicular à linha neutra no eixo ) vai ser .
Segundo, o momento em relação ao eixo também vai gerar uma tensão normal de flexão .
Pela regra da mão direita, conseguimos ver que esse momento é positivo (por estar no sentido do eixo ):
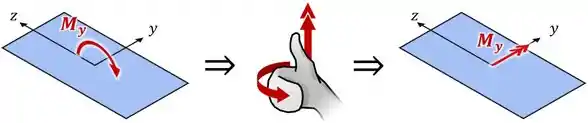
E pelo desenho dele, vemos que ele gera compressão na parte direita da coluna (com posição em relação ao eixo negativa) e tração na esquerda (com posição em relação ao eixo positiva):
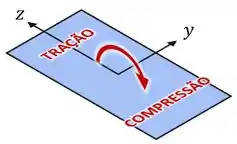
Então, para descrever a tensão devido ao momento , queremos uma fórmula:
- Semelhante à fórmula da flexão que conhecemos ;
- Mas que seja relativa ao momento , à posição em relação à linha neutra no eixo e ao momento de inércia da área em relação ao eixo , ;
- E que, para valores positivos de , resulte em valores de positivos (de tração) para valores positivos da posição e valores de negativos (de compressão) para valores negativos da posição .
Dessa forma, a nossa fórmula da flexão para o momento fica assim:
Sendo que pode ser calculado pela fórmula , mas dessa vez com uma base (paralela à linha neutra no eixo ) e uma altura (perpendicular à linha neutra no eixo ) .
Por último, nós temos que a força axial de compressão vai gerar na coluna uma força normal interna .
Sendo que a tensão gerada por essa força normal pode ser descrita pela fórmula:
Onde é a área da seção transversal da coluna.
O que tudo isso significa é que...
Para saber a tensão normal nessa coluna, podemos fazer a superposição de efeitos desses três carregamentos (momento em , momento em , e compressão ) para encontrarmos que:
Sendo que normalmente essa fórmula é escrita reorganizada assim:
E o que é que o exercício quer?
Ele quer que a gente determine a tensão máxima nessa coluna.
Daí que observando a fórmula acima para , vemos que:
1. O termo vai ter um valor sempre de compressão (), uma vez que .
2. O termo assume seu valor máximo de compressão () para , no “topo da seção”, e seu valor máximo de tração () para , na “base da seção”.
& 3. O termo assume seu valor máximo de compressão () para , na “direita da seção”, e seu valor máximo de tração () para , na “esquerda da seção”.
Dessa forma, a tensão máxima nessa coluna vai ser uma tensão de compressão no ponto de sua seção de posição e :
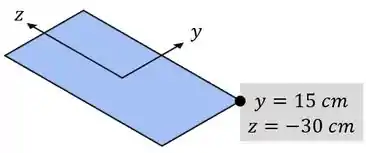
Isso porque esse é o único ponto em que vamos ter a...
- (1.) Compressão uniforme devido à força normal
- (2.) Compressão máxima devido à
- (3.) Compressão máxima devido à .
- Calcular os momentos e e o esforço interno normal gerados pela nossa carga excêntrica;
- Calcular as propriedades geométricas , e para a seção transversal da nossa coluna;
- & aplicar a fórmula para o ponto de compressão máxima na coluna.
Colaborando com a...
Colaborando com a...
Então, para resolver o exercício, devemos:
Passo 2
Agora que a gente já entendeu e revisou tudo que está rolando no exercício, podemos seguir direto para uma resolução bem rápida dele.
Primeiro, vamos calcular os momentos e e o esforço interno normal gerados pela nossa carga excêntrica.
Observando a nossa plataforma:
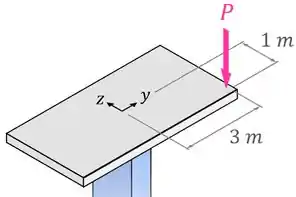
Vemos que o momento em relação ao eixo , vai ser gerado com um braço de e vai ter um valor positivo, por estar no sentido do eixo de acordo com a regra da mão direita.
Dessa forma, vamos ter que:
E também vemos que o momento vai ser gerado com um braço de e vai ter um valor positivo, por estar no sentido do eixo de acordo com a regra da mão direita.
Dessa forma, temos que:
Por fim, como a força é de compressão, ela vai gerar uma força interna normal :
Passo 3
Em seguida, vamos calcular as propriedades geométricas para seção transversal da coluna, observando as dimensões indicadas pelo exercício:
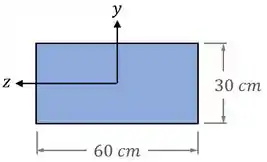
Quanto à área , temos:
Quanto ao momento de inércia da área em relação ao eixo , , vamos ter uma base (paralela à linha neutra no eixo ) e uma altura (perpendicular à linha neutra) .
Então:
Já para , o eixo da linha neutra troca e as dimensões também: a base paralela à linha neutra no eixo vai ser e a altura perpendicular à linha neutra vai ser :
Passo 4
Agora, só falta aplicar a fórmula:
...para o ponto de compressão máxima para encontrarmos a tensão normal máxima nessa coluna.
Aplicando essa fórmula e substituindo nela:
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- & ,
...vamos encontrar a nossa tensão normal máxima na coluna:
Calculando cada termo, temos:
E somando tudo, encontramos que:
Convertendo esse resultado para temos:
Aí, na hora de fornecer nosso resultado final, o fornecemos como um valor absoluto e indicamos que é uma tensão de compressão: