Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Condições de Contorno

Ver Teoria
Exercício 51234678

Enunciado

(Adaptada) Um líquido viscoso enche o espaço anular entre dois cilindros concêntricos verticais. O cilindro interno é estacionário e o cilindro externo gira com velocidade constante. O escoamento é laminar. A equação simplificada de Navier-Stokes está indicada abaixo. Obtenha expressões para o perfil de velocidades do líquido.

Equação da Navier-Stokes simplificada

d d r 1 r d d r r v θ = 0

Passo 1

Vamos começar entendendo melhor esse espaço anular? Essa figura ilustra o escoamento:

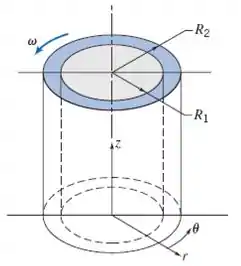
Os cilindros são concêntricos, sendo que o de dentro está parado e o de fora está girando. Com isso, temos as condições de contorno!

Afinal, qual delas? Iremos aplicar nos cilindros a condição de não-deslizamento, beleza? Vamos lá

No cilindro interno, ou seja, em r =   R 1 , pela condição de não-deslizamento, o fluido estará parado, pois o cilindro de dentro está parado. Logo,

v θ ( R 1 ) = 0

Olhando para o cilindro externo, ou seja, em r = R 2 , por essa mesma condição (a de não deslizamento), a velocidade do fluido será...

v θ ( R 2 ) = ω R 2

Dessa vez, a velocidade não é zero, pois o cilindro de fora está se movendo. Ele se move justamente com essa velocidade 😊

Beleza! Agora que sabemos as condições de contorno, vamos dar uma olhadinha na equação que o enunciado deu.

Passo 2

A equação de Navier-Stokes simplificada é

d d r 1 r d d r r v θ = 0

Como queremos encontrar o perfil de velocidades, precisamos integrar essa equação.

Integrando

1 r d d r r v θ = c 1

d d r r v θ = c 1 r

Integrando de novo:

r v θ = c 1 r 2 2 + c 2  

Isolando v θ , já que queremos saber o perfil de velocidades

v θ = c 1 r 2 + c 2 1 r

Opa! Vamos descobrir essas constantes c 1 e c 2 agora!

Passo 3

Para descobrir essas constantes, vamos usar as condições de contorno. No cilindro de dentro, temos a condição de contorno v θ ( R 1 ) = 0

Substituindo no perfil de velocidade

v θ = c 1 r 2 + c 2 1 r

0 = c 1 R 1 2 + c 2 R 1

Arrumando

c 1 . R 1 2 = - c 2 R 1

c 1 = - 2 c 2 R 1 2

Ok! Encontramos uma expressão relacionando as duas constantes c1 e c2. Vamos em busca de outra expressão através da segunda condição de contorno (a do cilindro externo)

v θ ( R 2 ) = ω R 2

Substituindo no perfil de velocidade

ω R 2 = c 1 R 2 2 + c 2 R 2

ω = c 1 2 + c 2 R 2 2

Isolando c 1

c 1 2 = ω - c 2 R 2 2

c 1 = 2 ω - 2 c 2 R 2 2

Yes! Encontramos duas expressões descrevendo c 1 em função de c 2 . Igualando as duas expressões

- 2 c 2 R 1 2 = 2 ω - 2 c 2 R 2 2

Isolando c 2 :

c 2 R 2 2 - c 2 R 1 2 = ω

R 1 2 c 2 - R 2 2 c 2 R 2 2 R 1 2 = ω

c 2 R 1 2 - R 2 2 R 2 2 R 1 2 = ω

c 2 = ω   R 2 2 R 1 2 R 1 2 - R 2 2

Substituindo em uma equação de c1

c 1 = - 2 R 1 2 c 2 = - 2 R 1 2   ω   R 2 2 R 1 2 - R 2 2

c 1 = - 2 ω   R 2 2 R 1 2 - R 2 2

Finalmente, substituindo c 1   e   c 2 no perfil de velocidade:

v θ = - 2 ω   R 2 2 R 1 2 - R 2 2 r 2 + ω   R 2 2 R 1 2 R 1 2 - R 2 2 1 r

Arrumando a casa:

v θ =   ω   R 2 2 R 1 2 R 1 2 - R 2 2 1 r - ω r R 1 2

Encontramos o perfil de velocidade!

Resposta

Perfil de velocidade

v θ =   ω   R 2 2 R 1 2 R 1 2 - R 2 2 1 r - ω r R 1 2

Exercícios de Livros Relacionados

O método euleriano de análise do escoamento de fluidos é mais semelhante ao estudo de um sistema ou de um volume de controle? Explique.
Aproximamos o escoamento do ar em um acessório de aspirador de pó seguindo as componentes da velocidade no plano central (o plano x y ): u = - V ˙ x π L x 2 + y 2 + b 2 x 4 + 2 x 2 y 2 + 2 x 2 b 2 + y
Considerando a metade a montante x0 doo campo de escoamento do Problema 4-94 (escoamento sobre um cilindro circular) . Introduzindo um parâmetro chamado função de corrente ψ , que é constante ao longo
Considere um campo de escoamento em regime permanente e bidimensional cuja componente x da velocidade é dada por u = a + b x - c 2 Onde a ,b e c são constante com dimensões apropriadas. Com qual forma
Considere o campo de escoamento do Problema 4-94 (escoamento sobre um cilindro circular). Calcule as duas taxas de deformação linear no plano r θ ; ou seja, calcule ε r r e ε θ θ . Discuta se os segme