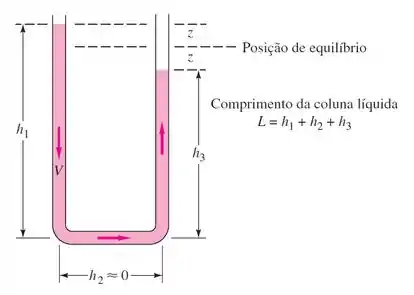
Exercícios Resolvidos de Condições de Contorno

Enunciado

Vamos analisar o escoamento oscilatório no tubo U da figura usando as equações completas da continuidade e de Navier-Stokes. Quais são as condições de contorno adequadas para resolver este problema?

Passo 1

Temos um escoamento oscilatório... o que isso significa?

Significa que nesse tubo em U existe uma situação inicial e outra final, e a coluna de líquido oscila para chegar na posição de equilíbrio. Então o escoamento nesse exercício não é permanente: o regime é transiente.

Ok! Então quais seriam as condições de contorno?

Como nosso regime é transiente, isto é, as propriedades variam com o tempo, nós precisamos conhecer as condições iniciais. Precisamos responder à pergunta: Em quais alturas z estão cada lado da coluna de líquido em t = 0?

Posicionando a referência

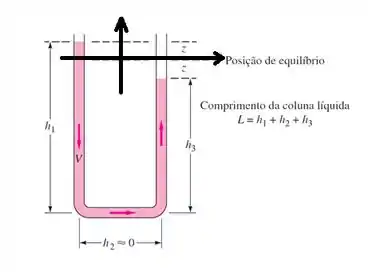
Além disso, vamos assumir que o sistema está inicialmente parado como condição inicial também

Passo 2

Até aqui definimos as condições iniciais do problema. Agora precisamos definir as condições de fronteira. Nesse problema temos 2 tipos de condições de fronteira

- Paredes (o tubo em U é uma barreira sólida ao escoamento)

- Interfaces (a coluna de líquido tem 2 interfaces com a atmosfera)

Nas paredes, onde o raio é o raio do tubo (r=R), pela condição de não deslizamento, a velocidade do fluido será zero

Além disso, na interface temos um sistema fluido/atmosfera. Considerando que a variação de altura da coluna não é brusca, a pressão do fluido é a pressão atmosférica nos pontos de interface

Com essas condições, conseguimos resolver o problema :D

Resposta

Condições iniciais

Condições de fronteira

Exercícios de Livros Relacionados

O método euleriano de análise do escoamento de fluidos é mais semelhante ao estudo de um sistema ou de um volume de controle? Explique.

Aproximamos o escoamento do ar em um acessório de aspirador de pó seguindo as componentes da velocidade no plano central (o plano x y ): u = - V ˙ x π L x 2 + y 2 + b 2 x 4 + 2 x 2 y 2 + 2 x 2 b 2 + y

Considerando a metade a montante x0 doo campo de escoamento do Problema 4-94 (escoamento sobre um cilindro circular) . Introduzindo um parâmetro chamado função de corrente ψ , que é constante ao longo

Considere um campo de escoamento em regime permanente e bidimensional cuja componente x da velocidade é dada por u = a + b x - c 2 Onde a ,b e c são constante com dimensões apropriadas. Com qual forma

Considere o campo de escoamento do Problema 4-94 (escoamento sobre um cilindro circular). Calcule as duas taxas de deformação linear no plano r θ ; ou seja, calcule ε r r e ε θ θ . Discuta se os segme