Os dois segmentos superiores do conjunto de barras esbeltas uniformes, soldadas em , têm uma massa por unidade de comprimento de , enquanto o segmento inferior tem uma massa de Localize o centro de massa do sistema.
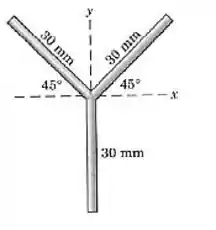
Passo 1
Vamos separar as partes que compõe a nossa figura:
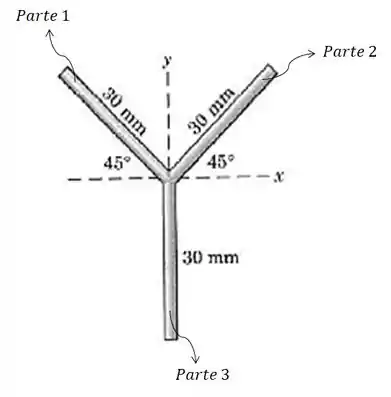
Passo 2
Vamos primeiro calcular a massa de uma das barras inclinadas. Perceba que elas têm um comprimento () de e que a massa de cada uma é dada por:
E a posição do centro dessas barras? Vamos desenhar um triângulo:
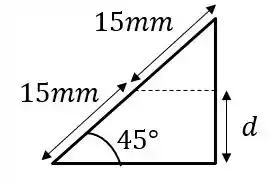
A distância vertical do centro:
Repare que a outra barra inclinada terá a mesma distância para o seu centro:
Passo 3
E a barra vertical de baixo? A sua massa será de:
E a posição do seu centro de massa está na metade do seu comprimento:
Repare que o sinal negativo é porque a coordenada está posicionada na parte negativa do eixo , ou seja, abaixo do zero.
Passo 4
Agora basta a gente usar a nossa fórmula de centro de massa para achar a coordenada :
Assim:
Show de bola? Percebeu que não convertemos para ? Isso porque todas as dimensões são dadas em !!!