O hemisfério homogêneo cuja porção central foi removida, é representado abaixo. Determine a coordenada do centro de massa do sistema.
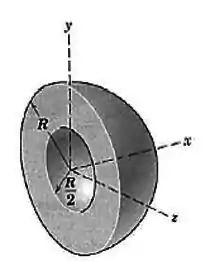
Passo 1
O volume de uma esfera é dado por:
Como estamos lidando com a metade de uma esfera de raio , o volume será dado por:
E seu centróide está localizado a uma distância do centro dada por:
Essa fórmula você pode encontrar em qualquer tabela!
Passo 2
Perceba que foi retirada uma semiesfera menor de raio da semiesfera maior. O volume desta semiesfera menor é:
Repare que este volume será negativo, pois estamos retirando a semiesfera menor da semiesfera maior.
E o seu centróide tem a seguinte coordenada :
Passo 3
Vamos montar a nossa tabela:

Precisamos terminar de preencher a tabela.
Vamos calcular o somatório dos volumes:
Passo 4
Nossa tabela está assim:
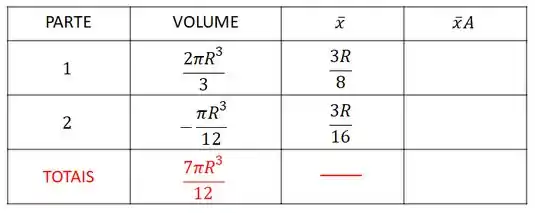
Temos que multiplicar cada volume pela sua respectiva coordenada :
E:
E o somatório destes dois valores que achamos é:
Passo 5
Então, a nossa tabela ficou:
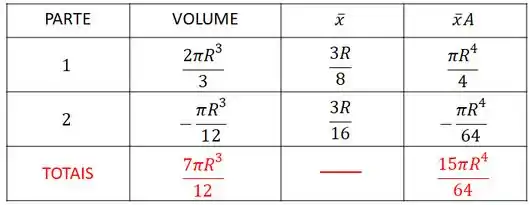
Agora é só aplicarmos nossa fórmula: