Sabendo que , determine a tensão máxima quando e .
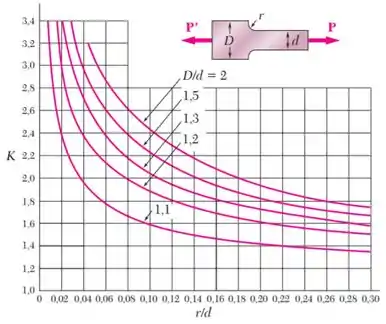
Observação: Use o gráfico abaixo para determinar o coeficiente de concentração de tensão :
Passo 1
O que está acontecendo?
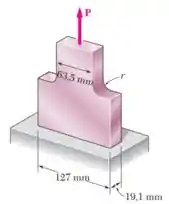
A peça tem dois segmentos, um de largura e outro de largura , sendo que existe um adoçamento de raio entre esses dois segmentos.
Além disso, a peça tem uma espessura e está submetida a uma tração , que gera ao longo de toda a peça uma força interna normal .
A maior tensão normal média nessa peça vai ocorrer no segmento de largura , já que ele vai possuir a menor área de seção transversal.
Mas por causa do adoçamento de raio , a tensão normal máxima na peça vai ser igual à essa tensão média vezes um coeficiente de concentração de tensões :
E o que é que o exercício quer?
Ele quer que a gente calcule essa tensão normal máxima na peça considerando que no item e que no item .
Para calcular essa tensão, vamos ter que calcular e usar o gráfico fornecido para determinar o valor do coeficiente em cada caso.
Passo 2
Então vamos começar calculando o valor da tensão normal média no segmento de largura .
Aplicando a fórmula da tensão normal média, temos:
Como esse segmento tem uma espessura e uma largura , a sua área de seção transversal vai ser igual à , então:
Substituindo os valores , e , encontramos que:
Reescrevendo isso em , que é o mesmo que , temos que:
Passo 3
Em seguida, vamos usar o gráfico fornecido para calcular o valor do coeficiente nas situações em que e em que .
Primeiro, precisamos calcular a razão para sabermos que curva do gráfico devemos usar.
Fazendo esse cálculo, encontramos que:
O que significa que nós vamos usar a curva mais à direita do gráfico.
Em seguida, precisamos calcular a razão em cada caso para podermos identificar no gráfico o valor correspondente de .
Para o item , temos que:
Já para o item , temos que:
Inserindo esses valores no gráfico:
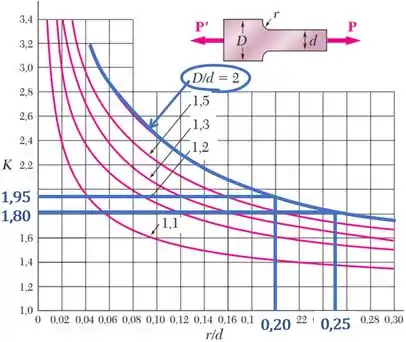
Encontramos que:
Passo 4
Encontrados os valores de e dos coeficientes , já podemos calcular as tensões máximas em cada caso.
Para o item , temos:
Substituindo os valores e , encontramos que:
Já para o item , temos que:
Substituindo e , encontramos:
E assim finalizamos o exercício!