Uma barra delgada de massa e comprimento é mantida na vertical com uma das extremidades apoiada no solo e depois é liberada. A extremidade superior atinge o solo sem que a extremidade de apoio deslize. Utilize que .
A velocidade da extremidade superior da barra imediatamente antes de tocar o solo é:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Passo 1
Vamos olhar para as forças sobre a barra:
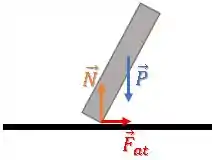
Repara que tanto a força normal quanto a força de atrito estão aplicadas sobre o ponto de apoio da barra com o chão.
Como esse ponto não desliza, ele não se move em todo o movimento de queda, a barra rotaciona sobre ele.
Então, essas forças não realizam trabalho:
Ahh belezaa... mas e daí?
Bom se as forças não conservativas e não realizam trabalho, elas não retiram energia do sistema.
Só resta a força peso , que é uma força conservativa.
Então, a energia mecânica do sistema se conserva e podemos usar isso para encontrar a velocidade angular da barra. A partir disso, podemos encontrar a velocidade de qualquer ponto da barra.
Passo 2
Inicalmente, a barra está parada, então ela não tem energia cinética, sobrando apenas a energia potencial gravitacional .
A altura será a altura do centro de massa da barra:
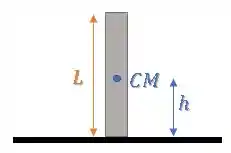
Considerando a barra homogênea (não temos nenhuma info sobre uma distribuição diferente), achamos que o centro de massa está na metade da barra, logo:
Então:
Passo 3
Enquanto no final, a barra terá apenas uma energia cinética associada à sua rotação:
O momento de inércia de uma barra fina é dado por:
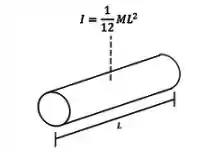
Porém, esse é o momento de inércia com relação a um eixo passando pelo centro da barra (centro de massa).
No nosso problema, o eixo está passando na extremidade (ponto de apoio), então devemos usar o teorema dos eixos paralelos para achar esse :
A distância entre os eixos é metade do comprimento da barra:
Substituindo isso, temos:
Passo 4
Voltando à equação das energias, temos:
Cortando e :
Passo 5
Achamos a velocidade angular , que é a mesma para todos os pontos da barra.
Portanto, podemos achar a velocidade linear de qualquer ponto da barra com:
Para o ponto na extremidade da barra, sua distância ao eixo de rotação é igual ao comprimento da barra, então:
Substituindo os valores, temos:
Ficamos com a alternativa (b).
Resposta
Letra (b)