A barra uniforme de massa e comprimento é sustentada no plano vertical por duas molas idênticas com rigidez e comprimidas de um comprimento na posição vertical, . Determine a rigidez mínima que garantirá uma posição de equilíbrio estável com Pode-se considerar que as molas atuam na direção horizontal durante um pequeno movimento angular da barra.
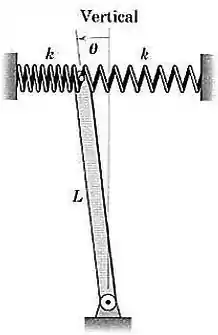
Passo 1
Podemos desenhar melhor esse problema assim:
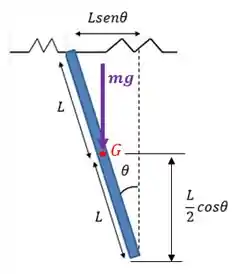
Onde é o centro de gravidade da nossa barra!
Nós temos duas molas, não é mesmo? Quando a barra se deslocar em radianos, uma mola será comprimida e a outra será distendida. Assim, podemos dizer que existem duas energias potenciais elásticas uma para cada mola.
Para a mola que será esticada, vamos ter que:
Mas quanto vale ? Repare que é o comprimento inicial da mola que foi dito no enunciado que é mais o quanto a mola esticou que pelo nosso desenho vale , então:
E para a mola que será comprimida teremos que o é o comprimento inicial da mola que também é menos o quanto a mola comprimiu que é o mesmo , então:
Não podemos esquecer da energia potencial gravitacional:
Lembrando que é a altura do centro de gravidade da barra!!!
Então, a nossa energia potencial total será a soma destas três formas de energias que achamos:
Passo 2
Agora precisamos derivar a nossa equação da energia total:
Repare que precisamos usar a regra da cadeia!
Será que a posição é uma posição de equilíbrio, como diz o enunciado? Para verificar isso temos que substituir na equação que acabamos de achar:
Então, é uma posição de equilíbrio!!!
Passo 3
Agora vamos verificar a estabilidade e para isso precisamos derivar duas vezes a nossa equação da energia total:
Passo 4
Para que o equilíbrio seja estável, devemos ter:
Então, vamos achar o valor de mínimo para que isto aconteça quando :
Então, o menor valor possível para a rigidez da mola deve ser igual a: