Um dos requisitos críticos no projeto de uma perna artificial é prevenir que a junta do joelho flambe sob carga quando a perna está esticada. Como uma primeira aproximação, simule a perna artificial como duas barras leves com uma mola de torção em seu ponto de união. A mola realiza um torque , que é proporcional ao ângulo de inclinação na junta. Determine o valor mínimo de que garantirá estabilidade da junta do joelho para .
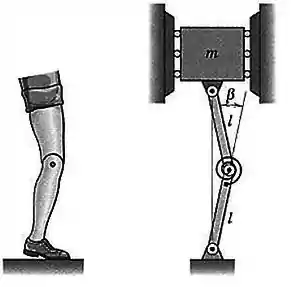
Passo 1
O sistema pode ser representado assim:
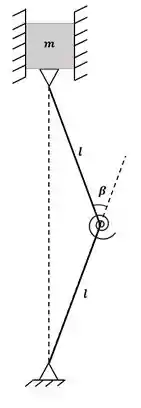
Mas repare que temos um triângulo com dois lados iguais a , então o triângulo é isósceles e tem dois ângulos iguais:
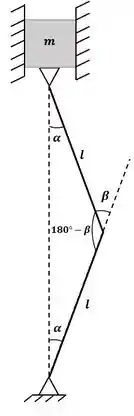
Repare que o maior ângulo do nosso triângulo isósceles é igual a:
E sabendo que a soma de todos os ângulos internos de um triângulo deve ser igual a , vamos ter que:
Beleza?
Então, teremos o seguinte sistema:
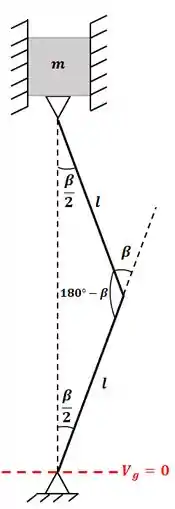
Vamos considerar o nosso referencial de energia potencial gravitacional nula como indicado na figura!!!
Passo 2
Temos duas energias potenciais...
A primeira é a energia potencial gravitacional:
O é a distância da massa até o nosso referencial, no nosso caso vamos ter que:
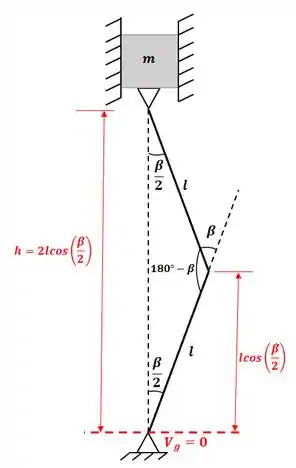
Então:
E a segunda é a energia potencial elástica:
Então, para acharmos a expressão da energia total é só somarmos cada uma das energias:
Passo 3
Agora precisamos derivar esta equação com relação ao ângulo :
Repare que tivemos que aplicar a regra da cadeia nesta derivada!
Para achar a posição de equilíbrio, temos que igualar a equação que achamos a zero:
Para obtermos zero como resultado, o valor de deve ser zero. Então, a nossa posição de equilíbrio é:
Passo 4
Agora queremos saber o valor mínimo de para que o equilíbrio seja estável. Então, vamos ter que derivar duas vezes a nossa equação da energia potencial total:
Repare que tivemos que aplicar a regra da cadeia nesta derivada!
Sabemos que nossa posição de equilíbrio é , então vamos substituir isso na equação que acabamos de achar:
Para que o equilíbrio seja estável vamos ter que:
Então, o valor mínimo de será: