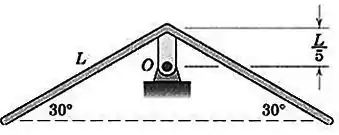
Duas barras idênticas estão soldadas em um ângulo de e são articuladas em , como mostrado. A massa do apoio é pequena em comparação à massa das barras. Investigue a estabilidade da posição de equilíbrio mostrada.
Passo 1
Vamos considerar a massa das duas barras juntas igual a . Então, cada barrinha terá a metade desta massa:
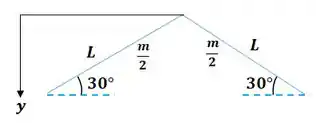
Não se esqueça que a massa do apoio é desprezível!!!
Vamos primeiro determinar o centro de gravidade do conjunto usando esta fórmula aqui:
Repare que é:
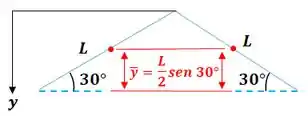
Então, vamos ter que:
Passo 2
A força de reação está sendo aplicada em . Assim, vamos calcular a energia potencial do corpo em relação ao ponto :
Esse é a distância vertical do centro de gravidade até o ponto que é a nossa referência:
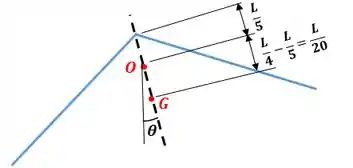
Então, vamos ter que:
Repare que o sinal negativo é porque estamos indo contra o sentido do eixo que criamos!
Agora podemos calcular a energia potencial do corpo em relação ao ponto :
Passo 3
Agora vamos calcular a derivada da energia potencial em relação ao ângulo:
Para vamos ter que:
Agora vamos derivar mais uma vez a equação que achamos:
Para vamos ter que:
Então, a estrutura está estável!!!