Análise por Semelhança
Teoria
Análise Dimensional e Similaridade
“Senhores passageiros, bem-vindos a bordo!”
E aííí, passageiro do Responde Aí! Você já parou para pensar como os pesquisadores começam em escala de laboratório (com modelos bem pequenininhos) e depois surge um aviãozão enorme? Daqueles que dá um friozinho na barriga só de pensar em decolar, hahaha
Para tranquilizar seu coração, o que está por trás disso não é mágica não. É uma técnica muito útil chamada Análise por Semelhança ou Similaridade.
Aqui em Mecânica dos Fluidos, vimos que o escoamento depende de muitas variáveis, certo? Viscosidade, massa específica, diâmetro, pressão, ... enfim! Dependendo do escoamento que estamos analisando, teremos certas variáveis que serão importantes
Na prática, o que acontece é o seguinte. Antes de fazer o protótipo de um avião, seria legal fazer um modelinho pequeno para testar. Mas e aí? Qual tamanho fazer? Se a força é 10 N no modelo, quanto será a força no protótipo?
Como nem tudo na vida dá para resolver por regra de 3, é aí que entra a Análise por Semelhança! Ela dá um jeito de comparar as variáveis no modelo e no protótipo. 😊 E assim, fazendo experimentos com o aviãozinho, conseguimos projetar a força no aviãozão.
Existem 3 principais tipos de semelhança e em um deles (o nosso principal e queridinho aqui) os números adimensionais vão resolver nossos problemas!
Tipos de semelhança
Os 3 tipos de semelhança (similaridade) são: geométrica, cinemática e dinâmica.
Semelhança geométrica
Para que o modelo (objeto menor) e o protótipo (objeto maior) tenham semelhança geométrica, eles precisam ter
- o mesmo formato e
- além disso, todas as dimensões do modelo devem ser relacionadas com as dimensões correspondentes no protótipo pelo mesmo fator de escala (exemplo em um retângulo: se a largura dobrou, o comprimento tem que dobrar também!)
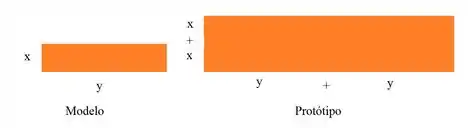
Um exemplo de similaridade geométrica são as maquetes!
Semelhança cinemática
Para dois escoamentos com similaridade cinemática, as velocidades em pontos correspondentes devem ter a mesma direção e sentido; já o módulo dessas velocidades mudam por um mesmo fator de escala :D
Com isso, em escoamentos semelhantes cinematicamente, as linhas de corrente estão relacionadas por um fator de escala constante. E o regime de escoamento é o mesmo 😉
Importante: escoamentos com semelhança cinemática tem semelhança geométrica.
Semelhança dinâmica
Por último, a semelhança mais desejada pelos pesquisadores do mundo inteiro, hahaha, a semelhança dinâmica. Qual é o diferencial dela?
A similaridade dinâmica acontece quando os mesmos tipos de forças no modelo são paralelos no protótipo e além disso, em todos os pontos correspondentes, os módulos das forças são relacionados por um mesmo fator de escala.
Importante: para que um escoamento tenha semelhança dinâmica, ele também tem semelhança cinemática e semelhança geométrica. A figura abaixo mostra o esquema:
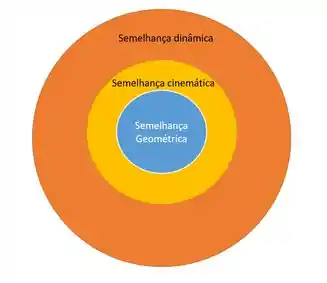
A semelhança geométrica sozinha não garante a semelhança cinemática. Nem a semelhança cinemática sozinha garante a dinâmica. Combinado? o/
Similaridade completa
A similaridade completa é quando temos os três tipos de semelhança juntos: geométrica, cinemática e dinâmica. Como a dinâmica engloba as outras 2, ela será a preferida. 😊
Então, quando o enunciado diz que há similaridade completa, ou então, que podemos considerar que entre o modelo e o protótipo temos semelhança dinâmica, o que isso significa?
Significa que podemos igualar os números adimensionais do modelo e do protótipo!! Exemplos:
E como os números adimensionais tem seus significados físicos, vamos conseguir relacionar as grandezas do modelo com as do protótipo. :D
Não dá para fazer por regra de 3 simplesmente, porque os números adimensionais mostram como é a influência de cada variável (se é diretamente proporcional, ou inversa, ao quadrado...). Isso é encontrado pelo Teorema Pi
E para te ajudar nos exercícios, aqui está uma lista dos números adimensionais mais usados em MecFlu! A dica é: ler o enunciado com carinho, anotar as variáveis informadas e as pedidas e escolher os números adimensionais que envolvam elas.
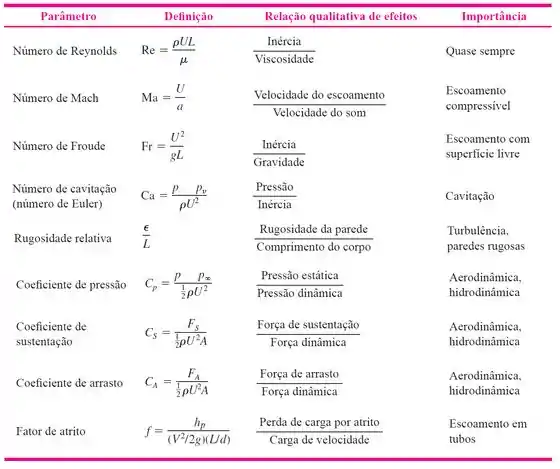
E é assim que damos o primeiro passo para projetar um avião. UAU! Vamos praticar isso aí? :)
Tipos de semelhança
Similaridade completa
Exercícios Resolvidos
Exercício Resolvido #1
Concurso Público IFRS– Área Engenharia Mecânica - 2013
Para ser de utilidade, um teste de modelo deve resultar em dados que possam, por meio de transposição em escala, fornecer forças, quantidades de movimento e cargas dinâmicas que existiriam no protótipo em tamanho real. Uma ferramenta matemática largamente utilizada na determinação de parâmetros para modelos de projetos é a análise dimensional. Que condições devem ser atendidas para assegurar a semelhança entre o modelo e o protótipo?
(A) Semelhança geométrica, semelhança cinemática e semelhança dinâmica
(B) Semelhança geométrica e semelhança cinemática
(C) Semelhança geométrica e semelhança dinâmica
(D) Semelhança cinemática e semelhança dinâmica
(E) Apenas a semelhança geométrica
Passo 1
Opaaa! Vamos começar os exercícios de análise por semelhança. Para garantir que o nosso objeto estudado é seguro e funciona direitinho numa escala diferente, precisamos que ele tenha uma relação de semelhança completa com o modelo!
Como vimos na teoria, a semelhança geométrica garante que a geometria irá mudar por um fator de escala. Mas isso não quer dizer que as velocidades serão similares também...
Por isso, além da semelhança geométrica, precisamos garantir a semelhança cinemática entre modelo e protótipo. Assim, garantimos a mesma direção e sentido das velocidades correspondentes, e o módulo é mudado por um fator de escala de velocidade
Maaas, ainda não acabamos! Precisamos a semelhança entre as dinâmicas de força para ter similaridade completa. E é justamente que a semelhança dinâmica nos dá 😉
Agora sim, sabemos que as semelhanças geométrica, cinemática e dinâmica devem ser buscadas para ter semelhança completa entre modelo e protótipo. Logo, a alternativa correta é a A.
Resposta
(A) Semelhança geométrica, semelhança cinemática e semelhança dinâmica
Exercício Resolvido #2
Concurso INMETRO (CESPE/UNB) – Pesquisador-tecnologista em Metrologia e Qualidade. Área: Metrologia em Mecânica dos Fluidos – 2009.
Considere um modelo geometricamente semelhante, com semelhança dinâmica completa, de um vertedouro a escoamento livre, em escala 1:9. Nesse caso, se a velocidade próxima à crista do vertedouro no modelo for de 0,3 m/s, então a velocidade correspondente no protótipo, em m/s, será igual a
(A) 0,03.
(B) 0,1.
(C) 0,9.
(D) 1.
(E) 2,7.
Passo 1
Nesse exercício, estamos trabalhando o caso mais usado em MecFlu: a semelhança dinâmica!
O enunciado garante que há semelhança dinâmica completa. Ou seja, podemos igualar os números adimensionais, além de usar o fator de escala da geometria. :D
O fator de escala foi dado e é 1:9. Com isso, já podemos dizer que o comprimento do protótipo é nove vezes o comprimento do modelo.
Beleza! Agora precisamos escolher um número adimensional para igualar. Como se trata de um escoamento livre, vamos na nossa tabela de números adimensionais e vemos que o número de Froude é importante para esse tipo de escoamento
Como temos semelhança completa:
Pela tabela:
Substituindo o fator de escala e a velocidade do modelo,
Simplificando:
A velocidade do protótipo é 0,9 m/s, como diz a letra C
Resposta
(C) 0,9.
Exercício Resolvido #3
White, F., Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH Editora, 2011, pp. 347, ex. P 5.84
(Adaptada) O protótipo da estrutura de uma plataforma oceânica deve enfrentar correntes de 150 cm/s e ondas com períodos de 12 s e 3 m de altura. Se um modelo na escala de 1:15 é testado em um canal de ondas, que velocidade de corrente deve ser encontrada no modelo?
Passo 1
Esse exercício quer calcular a velocidade do fluido que passa por uma plataforma oceânica. Nesse tipo de situação temos um escoamento com superfície livre e podemos usar o número de Froude.
Primeiro, vamos considerar semelhança dinâmica entre o modelo e o protótipo. Assim, poderemos calcular a a velocidade porque vamos igualar os números de Froude nos dois casos :D
Já que estamos falando muito nele, vou apresentar haha
Ou, então
Beleza, então igualando Froude do modelo e do protótipo
Dá para simplificar
Bem, até aí, sabemos a velocidade do protótipo, que é
Para achar a velocidade no modelo, precisamos da relação entre os comprimentos. No enunciado é 1:15, logo
Substituindo
Com isso, conseguimos calcular a velocidade no modelo
Resposta
Exercício Resolvido #4
White, F., Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH Editora, 2011, pp. 347, ex. P 5.80
O protótipo de uma embarcação de 35 m é projetado para uma velocidade de cruzeiro de 11 m/s (em torno de 21kn). Seu arrasto deve ser simulado em um modelo de 1 m de comprimento, em um tanque de reboque. Para a escala de Froude, encontrar (a) a velocidade de reboque, (b) a razão entre os arrastos do protótipo e do modelo (c) a razão entre as potências do protótipo e do modelo.
Passo 1
Opa! :D Temos aqui um modelo para fazer um protótipo de embarcação.
Para passar de um para o outro e descobrir velocidade, força e potência, vamos considerar que eles são similares dinamicamente, certo? o/
Considerando essa semelhança dinâmica, podemos usar a escala de Froude dita no enunciado. Ou seja: vamos igualar o número de Froude do protótipo e do modelo para encontrar a velocidade!
Lembrando que o número de Froude é essa carinha aqui:
Ou, podemos escrever também:
E o número de Froude do modelo é igual ao do protótipo:
Reorganizando isso aí e simplificando a gravidade:
Sabemos do enunciado que a razão entre os comprimentos é:
Então:
Já que o protótipo é projetado para velocidade 11 m/s, a velocidade do modelo é:
Passo 2
Para encontrar a razão entre as forças de arrasto do protótipo e do modelo, vamos usar o número adimensional coeficiente de arrasto .
Lembrando que consideramos no Passo 1 semelhança dinâmica. É por isso que podemos igualar o também, assim como fizemos com Froude.
Igualando:
Reorganizando a equação para colocar a razão que queremos encontrar do lado esquerdo, vamos ter:
Como nos dois casos é o mesmo fluido (mesma massa específica), podemos simplificar assim:
No Passo 1, descobrimos a razão entre as velocidades
Para encontrar a relação entre as áreas (área projetada na direção do escomento), vamos considerar uma embarcação com essa área quadrada, já que só temos a informação de comprimento da geometria.
A relação entre os comprimentos é 1:35. Logo,
Então, a razão entre os arrastos do modelo e do protótipo é 1:42875
Passo 3
Finalmente, vamos achar a razão entre as potências. Lembrando que a potência pode ser definida como força vezes a velocidade
Repara que a potência não é um número adimensional. Vamos achar a razão entre elas, substituindo os valores de força e velocidade que encontramos entre os passos.
Então a razão é
Dos passos 1 e 2, encontramos as razões entre as velocidades e forças
Logo, a razão entre as potências é
Resposta
Exercício Resolvido #5
White, F., Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH Editora, 2011, pp. 340, ex. P 5.4
Quando testada em água a 20°C escoando a 2 m/s, uma esfera de 8 cm de diâmetro apresenta um arrasto de 5 N. Qual será a velocidade e a força de arrasto sobre um balão meteorológico de 1,5 m de diâmetro atracado no ar nas condições padrão ao nível do mar sob condições dinamicamente semelhantes?
Passo 1
Primeiro passo que vamos fazer é organizar o que foi dado e o que foi pedido. Vamos lá? É importante notar que entre modelo e protótipo temos fluidos diferentes nesse exercício!
Água a 20°C (fluido usado no teste – modelo) :
Ar a nível do mar (fluido usado no balão – protótipo) :
Velocidade de teste (modelo) do fluido
Diâmetro da esfera de teste (modelo)
Diâmetro do balão (protótipo)
Força de arrasto no caso teste (modelo)
Com todos esse valores, precisamos calcular velocidade e força de arrasto no protótipo. Como há semelhança dinâmica, podemos igualar números adimensionais.
Passo 2
Pela similaridade dinâmica (e consequentemente cinemática) o regime de escoamento é o mesmo. Um número adimensional que diz respeito ao tipo de escoamento e que envolve velocidades e demais variáveis que já conhecemos é o número de Reynolds
Igualando
Substituindo o que já sabemos do enunciado
Então, a velocidade do ar no balão (protótipo) é
Opa! Encontramos a primeira pergunta do exercício
Passo 3
Para responder a segunda pergunta (Qual a força de arrasto no protótipo?) precisamos de um número adimensional que a englobe, certo?
Esse número é o coeficiente de arrasto.
Sendo V a velocidade do fluido e A a área projetada na direção do escoamento
A área projetada de uma esfera é ou . Então, para o modelo, temos a seguinte área
Por sua vez, a área projetada do balão também é um círculo. Logo, para o protótipo,
Pela semelhança dinâmica, igualamos o coeficiente de arrasto no modelo e no protótipo
Substituindo os valores que conhecemos até agora
Simplificando
Substituindo os diâmetros
Fazendo as contas
E assim, encontramos a força de arrasto no balão 😉
Resposta
Exercício Resolvido #6
White, F., Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH Editora, 2011, pp. 347, ex. P 5.81
(Adaptada) Um avião, de comprimento total de 16,8 m, é projetado para voar a 680 m/s a uma altitude padrão de 8.000 m. Um modelo na escala 1:30 deve ser testado em um túnel de vento com hélio pressurizado a 20°C. Qual é a pressão adequada do túnel em atm?
Dica: para similaridade em escoamentos supersônicos, usamos os números adimensionais Reynolds e Mach.
Passo 1
Vamos aprender a usar um novo número adimensional nesse exercício: o número de Mach
Mas antes de usá-lo vamos identificar as variáveis no modelo e no protótipo
Protótipo (avião):
- o protótipo está submetido ao ar a 8000 m de altitude, com isso
(velocidade do som)
Modelo:
- o modelo está submetido ao hélio a 20°C
(velocidade do som)
Não conhecemos a velocidade do modelo, nem a massa específica e queremos saber a pressão. Então, a estratégia é encontrar a velocidade pelo número de Mach, a velocidade por Reynolds e assim encontrar a pressão pela equação dos gases (pV=nRT) 😉
Mas calma, porque vamos passo a passo!
Passo 2
O número de Mach, conforme vimos na tabela de número adimensionais da teoria, é
Considerando a similaridade de escoamento supersônico e seguindo a dica do enunciado, vamos igualar o Mach do modelo e do protótipo
Substituindo os valores que conhecemos
Encontramos então a velocidade do modelo. Super alta! Vamos usá-la em Reynolds!
Passo 3
Também por similaridade podemos igualar o número de Reynolds do protótipo e do modelo. Assim, vamos descobrir a massa específica do Hélio nas condições do escoamento
Lembrando de Reynolds:
Igualando
Substituindo
Reorganizando
Com isso, encontramos que a massa específica do hélio nessas condições é
Passo 4
Agora que sabemos a massa específica do hélio, é hora de encontrar o que foi pedido no enunciado: a pressão. Para isso, vamos considerar a equação dos gases
Isolando a pressão
Sabendo que o número de mols é a massa sobre massa molar
Assim, relacionamos pressão e massa específica!
Usando a constante do gás Hélio R a 20°C (293 K)
E assim encontramos a pressão do Hélio nas condições do modelo!
Resposta
Exercício Resolvido #7
White, F., Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH Editora, 2011, pp. 345, ex. P 5.67
Um estudante precisa medir o arrasto sobre um protótipo de dimensão característica movendo-se à velocidade em ar nas condições atmosféricas padrão. Ele constrói um modelo de dimensão característica , de forma que a relação é um certo fator f. Ele então mede o arrasto sobre o modelo em condições dinamicamente semelhantes (também com ar nas condições atmosféricas padrão). O estudante afirma que a força de arrasto sobre o protótipo será idêntica àquela medida no modelo. Essa afirmação está correta? Explique.
Passo 1
Nesse exercício, temos que comparar a força de arrasto do modelo com a força de arrasto do protótipo.
O número adimensional que tem essa variável é o coeficiente de arrasto ! Olha aí
Sendo ρ a massa específica do fluido, U a velocidade do fluido (que no caso é o ar) e A a área projetada do objeto na direção do escoamento.
Como o enunciado diz que as condições entre modelo e protótipo são dinamicamente semelhantes, podemos igualar os coeficientes de arrasto
Assim,
Como no modelo e no protótipo, a massa específica se mantém pois é o mesmo fluido, podemos simplificar
Para encontrar a relação entre as forças de arrasto, precisamos saber as relações entre as velocidades e entre as áreas.
Passo 2
Começando pelas velocidades. :D
O enunciado garante que temos semelhança dinâmica, certo? Com isso, temos semelhana cinemática, o que significa que o regime de escoamento se mantém. Logo, o número de Reynolds no protótipo e no modelo é o mesmo!
Sendo que
Substituindo
Como é o mesmo fluido nos dois casos, a massa específica e a viscosidade dinâmica se mantém e podemos cortar
Daí, vamos lembrar que o enunciado deu a relação entre os diâmetros
O que nos dá
Logo, a relação entre as velocidades é
Substituindo na nossa igualdade entre os coeficientes de arrasto CD
Substituindo a relação das velocidades
Passo 3
Beleza! Agora é hora de analisar as áreas e assim encontrar a relação entre elas. Como a dimensão característica é d (ou seja, um diâmetro), o modelo e o protótipo são esferas!
A área projetada da esfera é ou . Substituindo
Simplificando
Lembrando que a relação entre os diâmetros é
Substituindo
Finalmente
Logo, o estudante estava certo! A força de arrasto do modelo é a mesma força de arrasto do protótipo!
Resposta
Sim, o estudante estava certo, pois pela análise por semelhança (dinâmica) verificamos que para esse caso, as forças de arrasto no modelo e no protótipo são iguais.
Exercício Resolvido #8
White, F., Mecânica dos Fluidos, 6ª ed. Porto Alegre: AMGH Editora, 2011, pp. 342, ex. P 5.34
Com uma boa aproximação, a condutividade térmica de um gás depende apenas da massa específica , do livre caminho médio , da constante do gás e da temperatura absoluta . Para o ar a e , e 6,5 E-8 m. Use essas informações para determinar o valor de para o hidrogênio a e se 1,2 E-7 m.
Passo 1
Esse problema envolve encontrar o grupo pi e também aplicar a análise por semelhança! Então, vamos lá encontrar o grupo pi!
Nosso problema pode ser escrito como:
De dimensões:
Temos cinco variáveis e quatro dimensões, logo temos pelo menos um grupo pi:
Isso não nos dá escolha a não ser como variáveis repetitivas.
Passo 2
Montamos nosso adimensional:
Logo nosso sistema fica:
Da equação 3:
Substituindo em 4:
Da equação 1:
Substituindo e na segunda equação:
Logo nosso pi é:
Passo 3
Agora, vamos considerar semelhança dinâmica entre as duas situações.
Para a situação 1, substituímos os valores do ar na expressão que encontramos, sem esquecer de converter a temperatura para de Celsius para Kelvin:
Igualando o número adimensional na situação com ar e a situação do hidrogênio, temos que: