Camada Limite
Produzido por Raphael EloiTeoria
Fala aí! Hoje vamos conversar sobre camada limite. Esse é um conceito fundamental para podermos discutir escoamentos externos!
⭐ Veja também ⭐
O que é a Camada Limite?
A camada limite é a região do escoamento afetada pela presença de uma superfície.
Pra entender melhor esse conceito, imagina um escoamento de ar ao redor da asa de um avião, como mostra essa ilustração aqui:
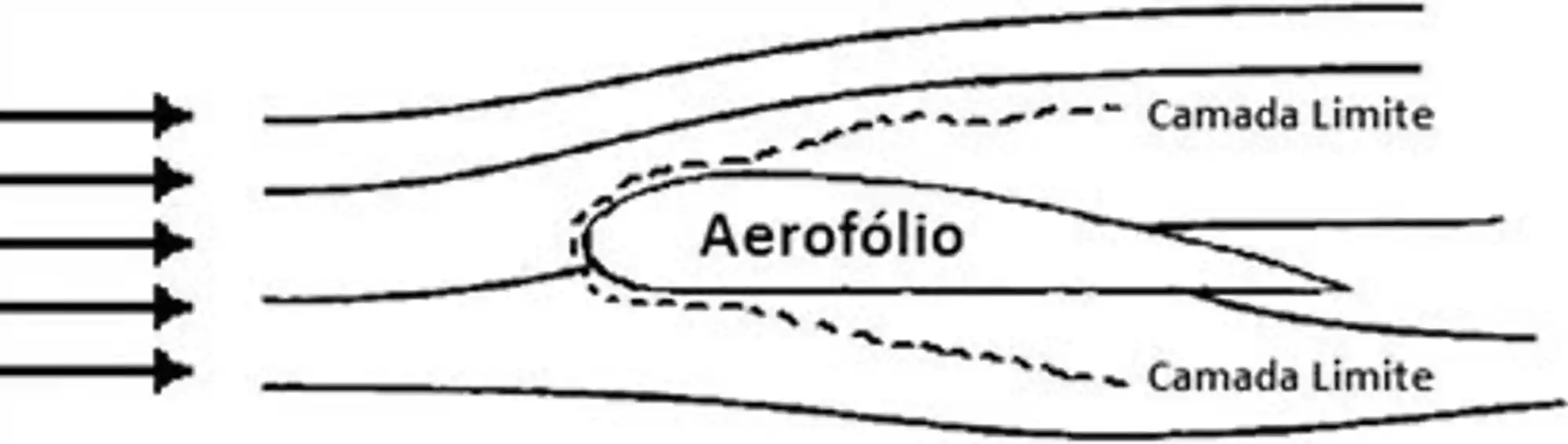
O fluido ali pertinho da asa do avião terá suas propriedades (como velocidade de escoamento e temperatura) afetadas, devido ao contato com a superfície do aerofólio.
Mas será que só as partículas de fluido que estão ali coladinhas vão ser afetadas, ou as que só estão próximas à superfície também?
Gradiente de Velocidade
O que acontece é o seguinte:
1️⃣ A velocidade da camada que está imediatamente em contato com a superfície se torna igual à velocidade desta.
2️⃣ A camada de fluido que está parada (em relação à superfície) interage com a camada vizinha logo acima de modo a desacelerar seu movimento.
3️⃣ Essa segunda camada interage com a camada acima dela, o que afeta o movimento desta outra.
4️⃣ Já pegou a ideia, né?
Só que tem um detalhe, esse fenômeno de desaceleração se torna mais fraco cada vez que passa para uma nova camada, ou seja, conforme se afasta da superfície.
Como as camadas de fluido mais próximas da parede têm velocidades menores que as mais afastadas, cria-se o que a gente chama de gradiente de velocidades.
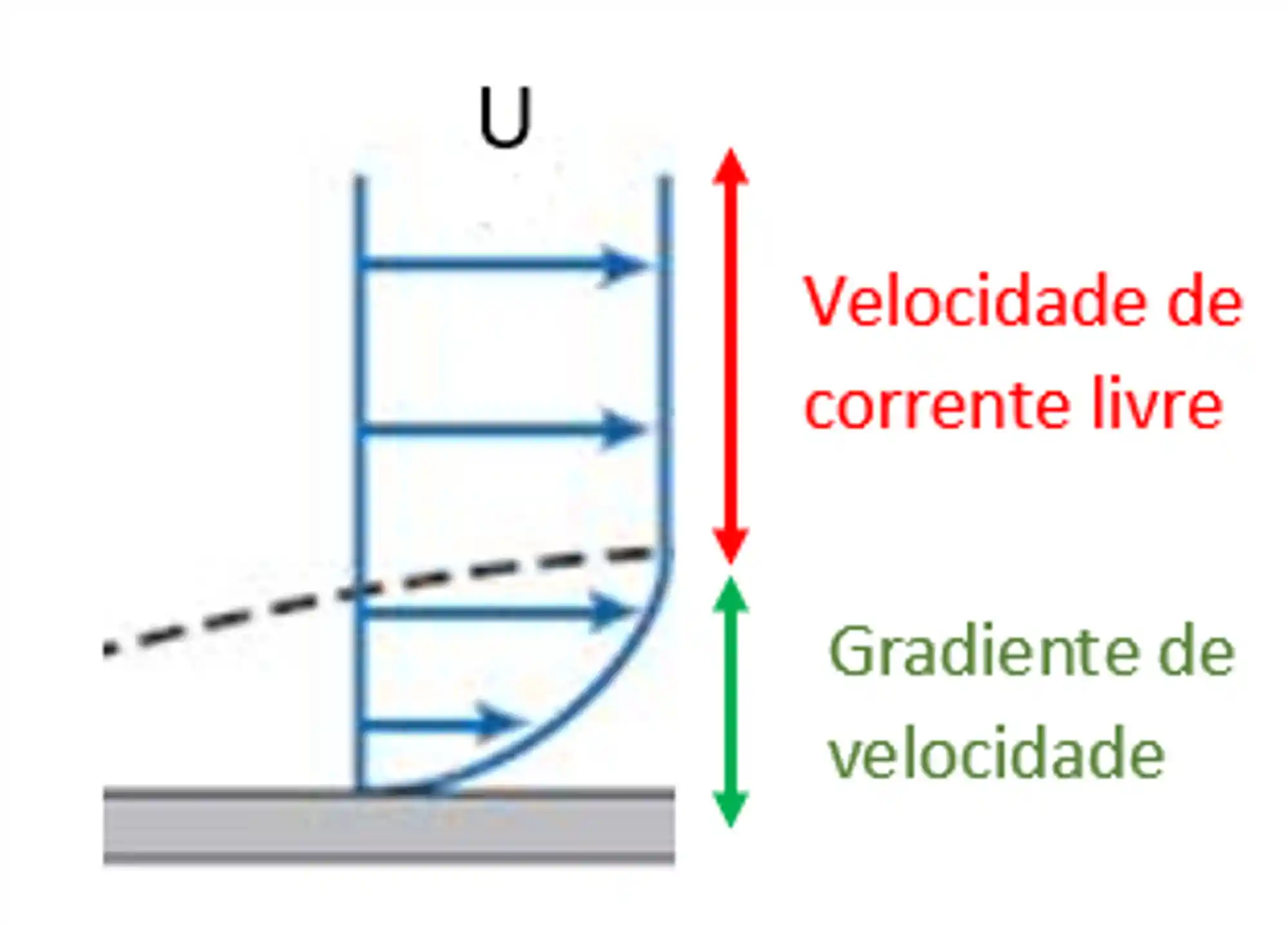
Mas o que é que causa esse gradiente de velocidade? São as forças viscosas entre as camadas e a superfície!
Então, a gente tem que lembrar da lei de Newton da viscosidade:
👉
👉
👉
Regiões da Camada Limite: Laminar e Turbulento
Se liga nessa imagem aqui:
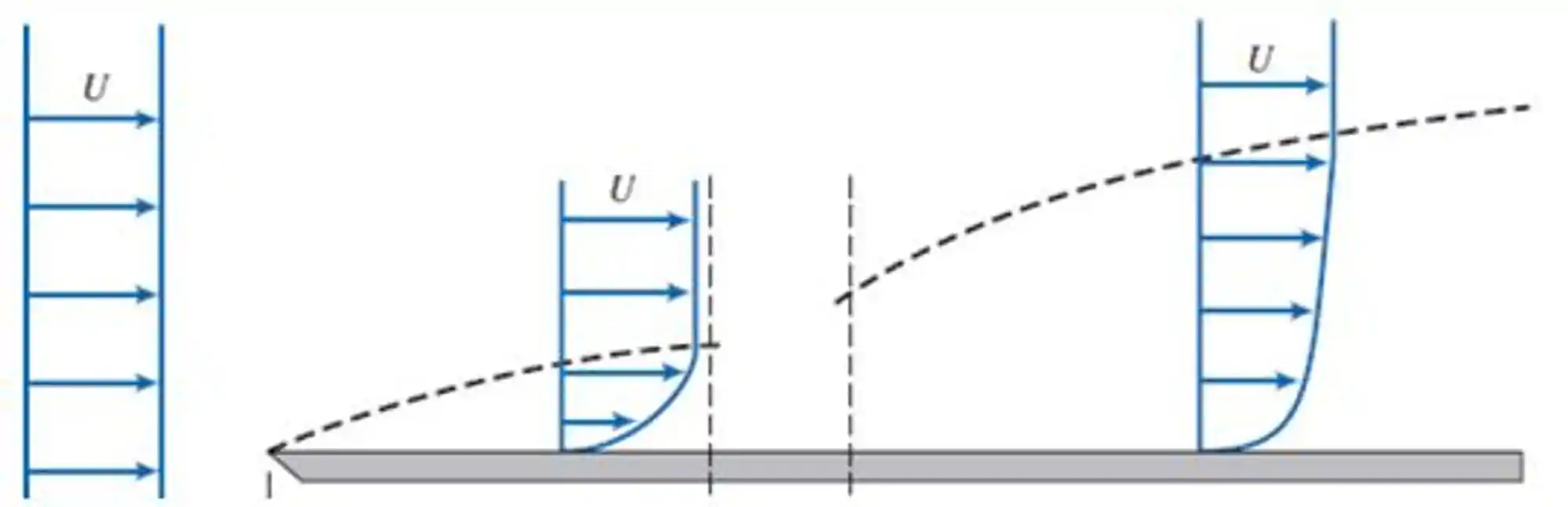
Essas setinhas azuis representam os perfis de velocidade.
A camada limite é tudo o que está abaixo daquela linha pontilhada. Repare como ela aumenta conforme o fluido escoa. Isso ocorre porque mais camadas são desaceleradas ao longo desse processo.
Velocidade de escoamento está relacionada com um tal de número de Reynolds! Então bora falar um pouco sobre ele
Número de Reynolds
O número de Reynolds serve para identificar se um escoamento é laminar ou turbulento. Ele depende da geometria do problema e, neste caso, é dado por:
Essa expressão relaciona a densidade (
Aí é o seguinte: se
O valor crítico para comparação depende de onde ocorre o escoamento. Se liga:
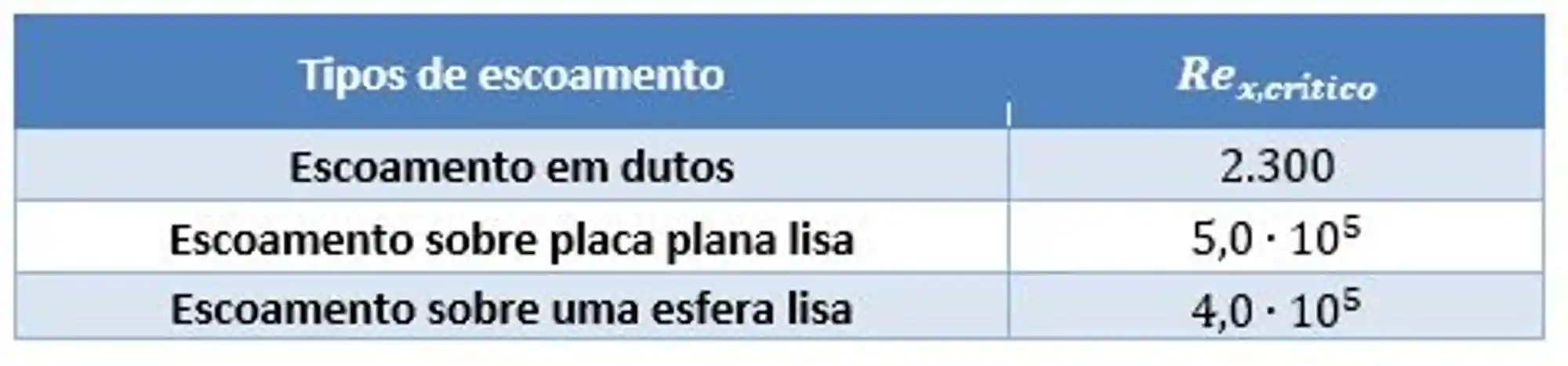
Nessa imagem aqui, a gente consegue perceber como ocorre a transição de um regime de escoamento para o outro:
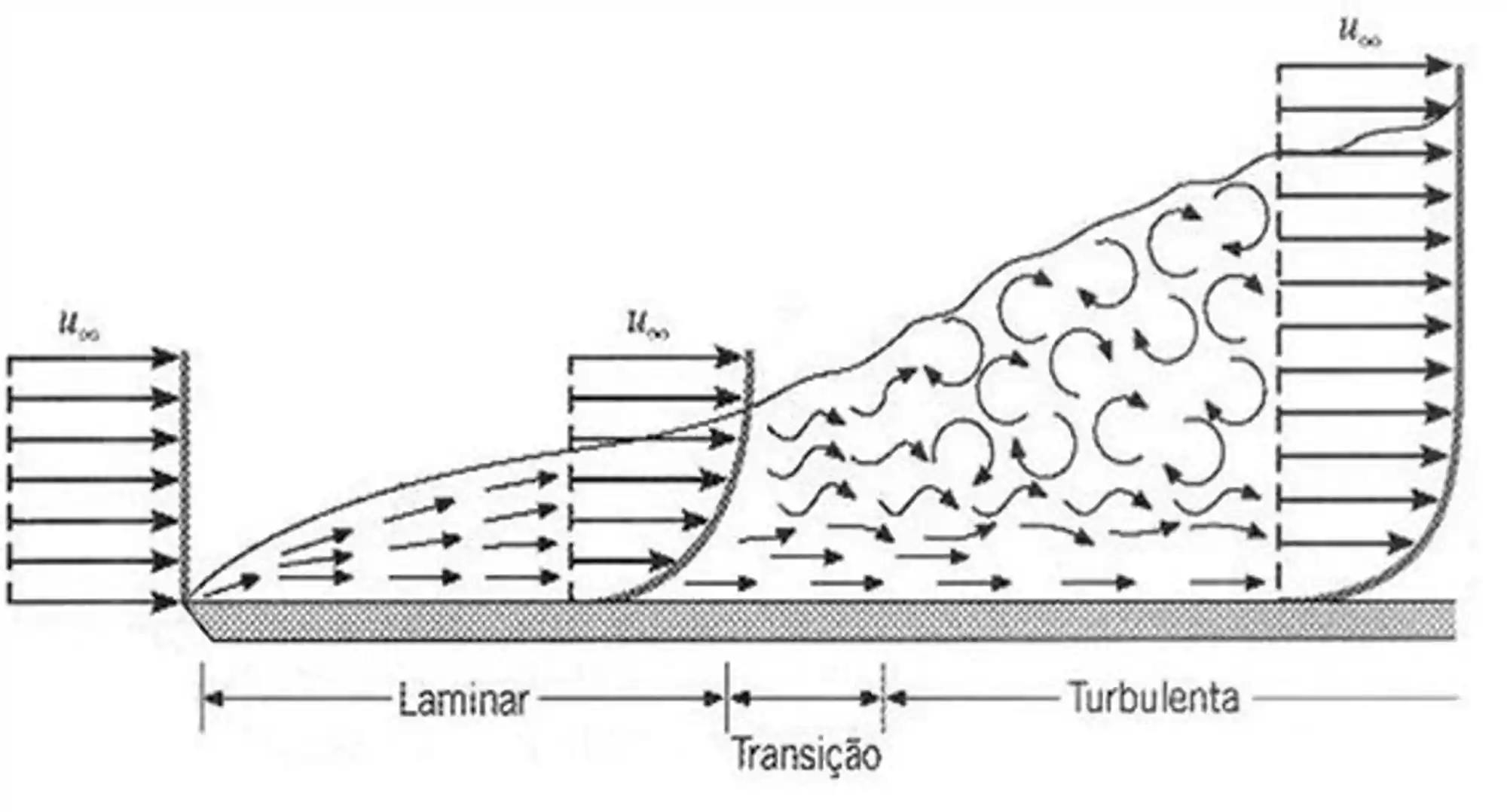
O segredo dos exercícios vai ser identificar a geometria do problema pra saber qual valor crítico usar para o número de Reynolds. Aí é só substituir na fórmula e correr pro abraço!