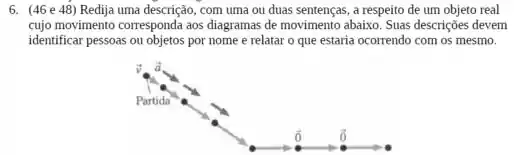
Exercícios de Movimento Retilíneo Uniformemente Variado - Lista de Exercícios Resolvida
Questão 1
Um elétron possui uma aceleração constante de . Em certo instante, sua velocidade é . Qual é sua velocidade antes e depois do instante considerado?
Ver solução completaQuestão 2
Ao ser lançado pela catapulta da plataforma de um porta-aviões, um caça a jato atinge a velocidade de decolagem de em uma distância aproximada de . Suponha aceleração constante.
- Calcule a aceleração do caça em
- Calcule o tempo necessário para o caça atingir essa velocidade de decolagem.
Questão 3
Um veículo elétrico parte do repouso e acelera em linha reta a uma taxa de até atingir a velocidade de . Em seguida, o veículo desacelera a uma taxa constante de até parar. Quanto tempo transcorre entre a partida e a parada? Qual é a distância percorrida pelo veículo desde a partida até a parada?
Ver solução completaQuestão 4
No instante em que um sinal de trânsito fica verde um automóvel começa a se mover com uma aceleração constante de No mesmo instante um caminhão, que se move com uma velocidade constante de , ultrapassa o automóvel. A que distância do sinal o automóvel alcança o caminhão? Qual é a velocidade do automóvel nesse instante?
Ver solução completaQuestão 5
Na figura, um carro vermelho e um carro verde, iguais exceto pela cor, movem-se um em direção ao outro em pistas vizinhas e paralelas a um eixo . Em , o carro vermelho está em e o carro verde está em . Se o carro vermelho tem uma velocidade constante de os carros se cruzam em se tem uma velocidade constante de eles se cruzam em Quais são a velocidade inicial e a aceleração do carro verde?

Questão 6
Um carro se move ao longo do eixo por uma distância de , partindo do repouso em e terminando em repouso em . No primeiro quarto do percurso a aceleração é de . Nos outros três quartos a aceleração passa a ser . Quais são o tempo necessário para percorrer os e a velocidade máxima?
Ver solução completaQuestão 7
Um motociclista se dirige para o leste através de uma cidade do Estado do Rio de Janeiro e acelera sua moto após sair de um sinal. Sua aceleração é constante e igual a . Inicialmente ele está a a leste do sinal, movendo-se para leste a .
- Determine sua posição e velocidade para .
- Onde está o motociclista quando sua velocidade é de ?
Questão 8
A figura mostra o movimento de uma partícula que se move ao longo do eixo com aceleração constante. A escala vertical do gráfico é definida por . Quais são o módulo e o sentido da aceleração da partícula?
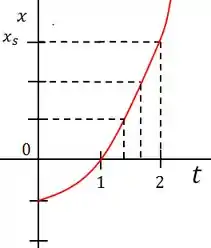
Questão 9
Três carros (A, B e C)estão em uma rodovia. O carro A é o mais massivo, com massa 4m e velocidade v. O carro B tem massa 2m e velocidade 2v e, por fim, o carro C tem massa m e velocidade 4v. Os três acionam os freios simultaneamente. Considere que os freios e os pneus dos 3 carros são idênticos, isto é, aplicam a força de frenagem máxima constante para cada carro. Qual carro percorre a maior distância desde o momento que os freios foram acionados até atingir o repouso?
a) Carro A
b) carro B
c) carro C
d) carros B e C
e) todos os três carros
Ver solução completaQuestão 11
2) Uma torneira mal fechada pinga uma gota a cada segundo sobre uma pia. Desprezando-se a resistência do ar, e considerando que as gotas caem a partir do repouso, avalie as afirmações a seguir:
I. Conforme as gotas caem, a distância entre elas aumenta;
II. Independente da altura da torneira, as gotas atingem a pia a uma taxa
de uma gota por segundo;
III. A velocidade final da gota ao atingir a pia depende da taxa com a
qual a torneira solta as gotas.
São verdadeiras:
(a) Apenas a I e II.
(b) Apenas a II e III.
(c) Apenas a I e III.
(d) Todas.
(e) Nenhuma.
Ver solução completaQuestão 12
5. Um carro está andando em linha reta com velocidade . No tempo , o carro está na origem. Posteriormente em o carro diminui sua velocidade até parar em . A aceleração do carro é dada em função do tempo por:
Onde é uma constante positiva que tem as dimensões de aceleração por unidade de tempo. •Descubra as funções posição e velocidade do carro em função do tempo. Expresse em termos das constantes apresentadas no exercício.
•Uma bicicleta está andando em uma velocidade no tempo a atrás do carro. O ciclista alcança o carro no momento que o carro para. Adote os seguintes valores para as constantes do problema , e . Descubra a velocidade da bicicleta e o momento que o carro parou.
Ver solução completaQuestão 14
Em qual das seguintes situações um carro numa estrada retilínea tem aceleração orientada para oeste?
(A) O carro movimenta-se para oeste com rapidez constante.
(B) O carro movimenta-se para leste com rapidez crescente.
(C) O carro movimenta-se para oeste com rapidez decrescente.
(D) O carro movimenta-se para leste com rapidez decrescente.
(E) O carro parte do repouso e move-se para leste.
Ver solução completaQuestão 15
Os movimentos de um carro e um caminhão ao longo de uma estrada em linha reta estão representados nos gráficos de velocidade versus tempo. Os dois veículos estão emparelhados no instante t = 0. Em um instante posterior , indique a sentença verdadeira sobre estes dois veículos.
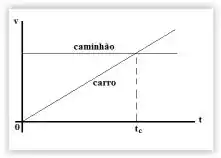
(A) O deslocamento do caminhão é maior do que o do carro.
(B) O deslocamento do carro é maior do que o do caminhão.
(C) O caminhão e o carro apresentam o mesmo deslocamento.
(D) O carro está ultrapassando o caminhão no instante .
(E) Nenhuma das sentenças acima é correta.
Ver solução completaQuestão 16
4) Um míssil é detectado por um satélite viajando de leste para oeste (L-O). A detecção é feita quando o míssil está a em uma direção que faz com o horizonte. O Satélite, então, acompanha o movimento do míssil no plano L-O por um ângulo de , quando a distância do míssil ao satélite é de . Desenho o esquema e calcule o deslocamento do míssil.
Ver solução completaQuestão 17
Em qual dos movimentos a seguir o módulo da aceleração é constante e diferente de zero ao longo do tempo:
- Movimento retilíneo uniformemente variado
- Movimento circular uniforme
- Movimento retilíneo uniforme
Escolha uma opção:
- Nenhuma das opções
- Todos os itens (i, ii e iii)
- i e ii
- Apenas iii
- i e iii
- Apenas ii
- Apenas i
Questão 18
Você está em um elevador panorâmico indo do andar térreo para o décimo primeiro andar quando, ao passar pelo segundo andar, que está a metros do andar térreo, percebe que uma lâmpada se soltou do teto do elevador. A lâmpada está a metros do piso do elevador e a velocidade constante do elevador é de . Assuma
a) Quanto tempo a lâmpada leva para bater no piso do elevador?
b) Uma pessoa posicionada no andar térreo observa a queda da lâmpada. Faça os gráficos de e que esta pessoa observou para o intervalo de até o tempo em que a lâmpada bate no chão do elevador.
c) Agora faça esses gráficos de e para a sua observação de dentro do elevador.
Ver solução completaQuestão 19
Q - Uma partícula desloca-se em movimento retilíneo sobre o eixo . Sabe-se que no instante ela encontra-se em e sua velocidade em função do tempo é dada por
onde as unidades estão no SI. Podemos afirmar que no instante , sua posição, em metros, é:
Ver solução completaQuestão 20
Um balde contendo água, com massa , é acelerado para cima por uma corda de massa desprezível que pode suportar (sem se partir) uma tensão máxima de . Se o balde parte do repouso, qual o tempo mínimo necessário para erguer o balde verticalmente a uma altura sem partir a corda?
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 21
Parte I - Uma pedra cai da janela de um prédio e passa diante da janela lateral (vertical) de um carro em movimento na rua. A pedra leva para percorrer a altura da janela. Sabendo que a janela do carro possui de altura e que sua extremidade inferior está a do solo, calcule a altura da qual a pedra caiu (medida em relação ao solo) e o tempo que ela leva para atingir o solo.
Ver solução completaQuestão 22
A partir de , um objeto move-se em linha reta com velocidade dada por , onde está em e em . Quando ele para momentaneamente, sua aceleração em é:
Questão 23
A velocidade de um automóvel é dada em pela expressão , onde é dado em segundos. As unidades de e são, respectivamente:
Questão 24
Um carro de corrida, que se move com aceleração constante, aumenta a sua velocidade de para , ao percorrer uma distância de metros. Em quanto tempo a distância de metros foi percorrida?
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 25
Um trenó e seu ocupante, com uma massa total de 85 kg, descem uma encosta e atingem
um trecho horizontal retilíneo com uma velocidade inicial de . Se uma força desacelera o trenó até o repouso a uma taxa constante de
- Que distância o trenó percorre até parar?
Questão 26
No trânsito de uma cidade podemos observar vários tipos de movimento. Em uma dessas situações encontramos parado em um sinal (farol) o veículo , quando o sinal abre este parte com uma aceleração constante de . Enquanto isso, um veículo , que mantinha uma velocidade constante de , consegue passar pelo sinal aberto mantendo a sua velocidade. Em que posição o veículo se encontra com o veículo , considerando a origem da trajetória como o local onde o sinal está e a estrada retilínea?
(a) ;
(b) ;
(c) Não se encontram;
(d) ;
(e) ;
Ver solução completaQuestão 27
Um carro, partindo do repouso, move-se com aceleração de durante . Desliga-se o motor, e o carro passa a ter movimento retardado, devido ao atrito, durante com aceleração de . Em seguida, os freios são aplicados e o carro para após . Qual a distância total percorrida pelo carro? Obs: Lembrem-se das equações para o movimento uniformemente variável: , e .
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 28
Dois automóveis A e B movem-se numa mesma rodovia e seus espaços variam com o tempo de acordo com as funções:
E
Com espaços medidos em km e tempos medidos em horas. Podemos afirmar que o tempo que os carros levarão para estar no mesmo ponto da estrada é:

(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 29
Em um tubo de óleo, é solta um a esfera que a cada segundos, desloca-se , sendo então, a velocidade que descreve o movimento sempre constante e igual a . Com base nessas informações, é correto afirmar que:
(a) a aceleração da esfera é constante.
(b) a velocidade constante caracteriza o movimento uniformemente variado.
(c) a velocidade constante caracteriza o movimento uniforme.
(d) o gráfico que descreve a velocidade da esfera é descrito por uma parábola.
(e) o movimento é uniforme porque a aceleração é constante.
Ver solução completaQuestão 30
Um objeto está se deslocando com velocidade de , no sentido positivo do eixo , quando passa a sofrer, em , uma aceleração dada por durante .
Qual a expressão da velocidade no intervalo ?
Ver solução completaQuestão 31
Um objeto está se deslocando com velocidade de , no sentido positivo do eixo , quando passa a sofrer, em , uma aceleração dada por durante .
c) Calcule sua aceleração média durante esses .
Ver solução completaQuestão 32
Um objeto está se deslocando com velocidade de , no sentido positivo do eixo , quando passa a sofrer, em , uma aceleração dada por durante .
Qual é o sentido dessa aceleração em relação ao eixo de referência?
Ver solução completaQuestão 33
Um objeto está se deslocando com velocidade de , no sentido positivo do eixo , quando passa a sofrer, em , uma aceleração dada por durante .
d) Determine a expressão da posição sabendo que em o corpo está passando pela posição .
Ver solução completaQuestão 34
Um objeto está se deslocando com velocidade de , no sentido positivo do eixo , quando passa a sofrer, em , uma aceleração dada por durante .
e) Calcule o deslocamento do corpo nos primeiros segundos do movimento;
Ver solução completaQuestão 35
Um objeto, partindo do repouso em , está se deslocando com velocidade ao longo do eixo . Nestas condições, pede-se:
b) O deslocamento do corpo no intervalo
Ver solução completaQuestão 36
Um objeto está se deslocando com velocidade de , no sentido positivo do eixo , quando passa a sofrer, em , uma aceleração dada por durante .
f) Calcule a velocidade média do objeto durante os segundos.
Ver solução completaQuestão 37
Um objeto, partindo do repouso em , está se deslocando com velocidade ao longo do eixo . Nestas condições, pede-se:
d) A distância total percorrida nos do movimento.
Ver solução completaQuestão 38
Na célebre corrida entre a lebre e a tartaruga, a velocidade da lebre é de e a da tartaruga de . A distância total a percorrer é de em linha reta. Depois de a lebre para e tira uma soneca de minutos, e depois acorda e continua com a mesma velocidade anterior de . Deixe todas as respostas em unidades do SI.
Quando a vencedora cruza a linha de chegada, qual a distância entre elas?
Ver solução completaQuestão 39
Na célebre corrida entre a lebre e a tartaruga, a velocidade da lebre é de e a da tartaruga de . A distância total a percorrer é de em linha reta. Depois de a lebre para e tira uma soneca de minutos, e depois acorda e continua com a mesma velocidade anterior de . Deixe todas as respostas em unidades do SI.
Qual o tempo máximo que a lebre poderia dormir e ainda assim ganhar a corrida?
Ver solução completaQuestão 40
Na célebre corrida entre a lebre e a tartaruga, a velocidade da lebre é de e a da tartaruga de . A distância total a percorrer é de em linha reta. Depois de a lebre para e tira uma soneca de minutos, e depois acorda e continua com a mesma velocidade anterior de . Deixe todas as respostas em unidades do SI.
Escreva as equações de movimento para a lebre e para a tartaruga.
Desenha as curvas da posição em função do tempo da tartaruga e da lebre (no mesmo gráfico). Quem ganha a corrida?
Ver solução completaQuestão 41
Na figura ao lado vê-se uma montagem. A bolinha de massa é lançada para cima por uma rampa que faz um ângulo com a horizontal, saindo da rampa a uma altura a partir do solo. Mede-se que a bolinha leva um tempo para atingir o solo, a partir do instante que sai da rampa.
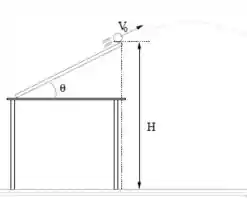
P1.1 – Calcule o módulo da velocidade da bolinha no instante que ela saiu da rampa, , em função de g, , , e .
Ver solução completaQuestão 42
Uma partícula inicialmente localizada na origem tem aceleração de e velocidade inicial . Qual é a posição da partícula em ?
Escolha uma opção:
- Nenhuma das alternativas
Questão 43
Uma jogadora de futebol chuta uma bola em uma direção de com o plano do campo. Depois de a bola toca o campo novamente. Qual é o alcance da bola? Desconsidere a resistência do ar, considere , .
Ver solução completaQuestão 44
Ao ser posicionada a uma distância de do centro de um prato giratório, o qual realiza duas voltas em , uma bolinha de não escorrega. Determine (b) o módulo e a orientação da aceleração centrípeta da bolinha.
Obs.: todas as respostas devem estar em unidades do SI.
Dica da prof.: para determinar a orientação tanto da aceleração centrípeta quanto da força centrípeta, basta dizer se são radiais para dentro ou para fora da circunferência.
Ver solução completaQuestão 45
Uma motocicleta se desloca com velocidade constante igual a . Quando o motociclista vê um a pessoa atravessar a rua, freia a moto até parar. Sabendo que a aceleração máxima para frear a moto tem valor absoluto igual a , e que a pessoa se encontra distante da motocicleta. O motociclista conseguirá frear totalmente a motocicleta antes de alcançar a pessoa?
Ver solução completaQuestão 48
38. Um passageiro de massa encontra-se de pé, em cima de uma balança, no interior de um elevador.
(a) Quanto marcará a balança se o elevador estiver em repouso ou em movimento retilíneo e uniforme?
Ver solução completaQuestão 49
38. Um passageiro de massa encontra-se de pé, em cima de uma balança, no interior de um elevador.
(c) Quanto marcaria a balança se o cabo se rompesse, fazendo com que o elevador se precipitasse em queda livre?
Ver solução completaQuestão 50
38. Um passageiro de massa encontra-se de pé, em cima de uma balança, no interior de um elevador.
(d) O que ocorreria se o elevador fosse puxado para baixo com uma aceleração de ?
Ver solução completaQuestão 51
38. Um passageiro de massa encontra-se de pé, em cima de uma balança, no interior de um elevador.
(b) Quanto marcará a balança se o elevador tiver uma aceleração:
i. dirigida para cima e de módulo ?
ii. dirigida para baixo e de módulo ?
Ver solução completaQuestão 52
Se um móvel percorre uma determinada trajetória com aceleração negativa e velocidade positiva, podemos afirmar que o tipo de movimento uniformemente variado percorrido pelo móvel neste caso é:
(a) movimento progressivo e retardado
(b) movimento retrógrado
(c) movimento retrógrado e retardado
(d) movimento circular e acelerado
(e) movimento progressivo e acelerado
Ver solução completaQuestão 53
Um trem parte de uma estação com aceleração constante de Um passageiro chega à estação segundos depois de o trem ter passado pelo mesmo ponto da plataforma. Qual é a menor velocidade constante que o passageiro deve correr para pegar o trem?
Resolva o problema de duas maneiras:
b) graficamente;
Ver solução completaQuestão 54
Q - Uma partícula desloca-se em movimento retilíneo sobre o eixo . Sabe-se que no instante ela encontra-se em e sua velocidade em função do tempo é dada por
onde as unidades estão no SI. Podemos afirmar que a distância percorrida pela partícula no intervalo é:
Ver solução completaQuestão 55
Q - Uma partícula desloca-se em movimento retilíneo sobre o eixo . Sabe-se que no instante ela encontra-se em e sua velocidade em função do tempo é dada por
onde as unidades estão no SI. Podemos afirmar que o deslocamento da partícula, em metros,
no intervalo é:
Ver solução completaQuestão 56
Um objeto, partindo do repouso em , está se deslocando com velocidade ao longo do eixo . Nestas condições, pede-se:
c) O tempo que ele leva para voltar à mesma posição, sabendo que partiu, em , da posição ;
Ver solução completaQuestão 57
Um trem parte de uma estação com aceleração constante de Um passageiro chega à estação segundos depois de o trem ter passado pelo mesmo ponto da plataforma. Qual é a menor velocidade constante que o passageiro deve correr para pegar o trem?
Resolva o problema de duas maneiras:
a) Analiticamente;
Ver solução completaQuestão 58
Um estudante está de pé sobre um penhasco vertical acima da entrada de uma caverna. Ele sente batendo no rosto um vento muito forte, e decide chutar uma bola horizontalmente, contra o vento, de forma que ela acabe caindo na entrada da caverna. Assuma que o vento vai gerar na bola uma aceleração horizontal de módulo , e assuma que, exceto por esse efeito, a resistência do ar na direção vertical pode ser desprezada.
Proponha uma fórmula para a velocidade com que o menino precisa chutar a bola para conseguir realizar seu feito.
Desenhe a forma aproximada os vetores velocidade e aceleração da bola no ponto em que a bola está mais distante da parede do penhasco.
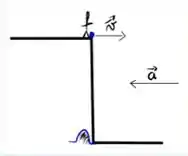
Questão 59
(Cap 2 – Ex 25) Suponha que uma nave espacial se move com uma aceleração constante de , o que dá aos tripulantes a ilusão de uma gravidade normal durante o voo.
(a) Se a nave parte do repouso, quanto tempo leva para atingir um décimo da velocidade da luz, que é 3,0 × m/s?
(b) Que distância a nave percorre nesse tempo?
Ver solução completaQuestão 60
(Capítulo 2.7 – Exercício 43) Você está discutindo no telefone celular enquanto segue um carro de polícia não identificado, a de distância; os dois veículos estão a . A discussão distrai sua atenção do carro de polícia por (tempo suficiente para você olhar para o telefone e exclamar: "Eu me recuso a fazer isso!"). No início desses , o policial freia bruscamente, com uma desaceleração de .
(a) Qual é a distância entre os dois carros quando você volta a prestar atenção no trânsito?
Suponha que você leve outros para perceber o perigo e começar a frear
(b) Se você também freia com uma desaceleração de , qual é a velocidade do seu carro quando você bate no carro de polícia?
Ver solução completaQuestão 61
(Capítulo 2.7 – Exercício 35) A Fig. mostra o movimento de uma partícula que se move ao longo do eixo x com aceleração constante. A escala vertical do gráfico é definida por. Quais são (a) o módulo e (b) o sentido da aceleração da partícula?
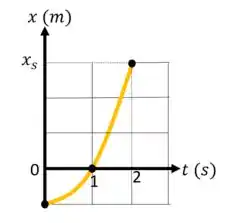
Questão 63
Uma Partícula movimenta-se em sentido contrário à orientação escolhida para sua trajetória.Partindo do repouso, ela adquire a velocidade de em apenas . Nesse intervalo de tempo podemos afirmar que seu movimento é:
(a) Progressivo acelerado
(b) Uniforme progressivo
(c) Acelerado retrógrado
(d) Retardado progressivo
(e) Progressivo retrógrado
Ver solução completaQuestão 65
Qual das seguintes situações não é possível?
(A) Um corpo tem velocidade nula e aceleração diferente de zero.
(B) Um corpo tem velocidade e aceleração em direção ao norte.
(C) Um corpo tem velocidade em direção ao norte e aceleração em direção ao sul.
(D) Um corpo tem velocidade constante e aceleração variando com o tempo.
(E) Um corpo tem aceleração constante e velocidade variando com o tempo.
Ver solução completaQuestão 66
Uma roda de bicicleta de raio está rolando sem deslizar ao longo de uma superfície horizontal. O centro de massa da bicicleta está se movendo com velocidade constante na direção positiva. Um chiclete está grudado na borda da roda. Assuma que em , o chiclete está localizado no topo da roda da bicicleta, ou seja,
Qual é o vetor posição do chiclete em função do tempo de acordo com um observador parado no chão?
Expresse sua resposta em termos das variáveis do exercício.
Ver solução completaQuestão 67
Um automóvel e um caminhão iniciam do repouso ao mesmo instante, com o automóvel inicialmente a alguma distância atrás do caminhão. O caminhão e o automóvel tem respectivamente acelerações de e . O automóvel ultrapassa o caminhão após este ter se movido .
Quanto tempo leva para o automóvel ultrapassar o caminhão?
Ver solução completaQuestão 68
Ignorando a resistência do ar em gotas de chuva, podemos considerar as gotas como objetos em queda livre.
As nuvens carregadas normalmente se localizam a algumas centenas de metros acima do chão. Calcule a velocidade que as gotas atingem o solo como se fossem objetos em queda livre. Dê sua estimativa em
Ver solução completaQuestão 69
Do topo de um prédio, um estudante arremessa um balão d’água verticalmente para baixo. O balão deixa a mão dele com velocidade igual a Desconsidere a resistência do ar para que o balão esteja em queda livre assim que abandona a mão do estudante.
Qual o módulo da velocidade após cair ?
Ver solução completaQuestão 70
Do topo de um prédio, um estudante arremessa um balão d’água verticalmente para baixo. O balão deixa a mão dele com velocidade igual a Desconsidere a resistência do ar para que o balão esteja em queda livre assim que abandona a mão do estudante.
Qual o deslocamento para os ?
Ver solução completaQuestão 71
Do topo de um prédio, um estudante arremessa um balão d’água verticalmente para baixo. O balão deixa a mão dele com velocidade igual a Desconsidere a resistência do ar para que o balão esteja em queda livre assim que abandona a mão do estudante.
Esboce os gráficos , , e para o movimento.
Ver solução completaQuestão 72
Um automóvel e um caminhão iniciam do repouso ao mesmo instante, com o automóvel inicialmente a alguma distância atrás do caminhão. O caminhão e o automóvel tem respectivamente acelerações de e . O automóvel ultrapassa o caminhão após este ter se movido .
Quão distante do caminhão o automóvel estava inicialmente?
Ver solução completaQuestão 73
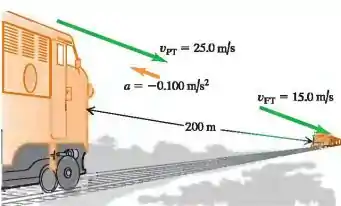
O engenheiro de um trem de passeio, viajando a , avista um vagão de carga adiante na mesma via (Figura abaixo). O vagão de carga viaja a na mesma direção que o trem de passeio. O engenheiro do trem freia imediatamente, com uma aceleração constante de , enquanto o vagão de carga se mantém com velocidade constante. Considere a posição da frente do trem quando o engenheiro aciona os freios.
Se acontecer, em que posição será?
Ver solução completaQuestão 74
Um automóvel e um caminhão iniciam do repouso ao mesmo instante, com o automóvel inicialmente a alguma distância atrás do caminhão. O caminhão e o automóvel tem respectivamente acelerações de e . O automóvel ultrapassa o caminhão após este ter se movido .
Em um único gráfico, rascunhe a posição de cada veículo em função do tempo.
Ver solução completaQuestão 75
Um automóvel e um caminhão iniciam do repouso ao mesmo instante, com o automóvel inicialmente a alguma distância atrás do caminhão. O caminhão e o automóvel tem respectivamente acelerações de e . O automóvel ultrapassa o caminhão após este ter se movido .
Qual a velocidade de cada um quando eles se encontram?
Ver solução completaQuestão 76
O engenheiro de um trem de passeio, viajando a , avista um vagão de carga adiante na mesma via (Figura abaixo). O vagão de carga viaja a na mesma direção que o trem de passeio. O engenheiro do trem freia imediatamente, com uma aceleração constante de , enquanto o vagão de carga se mantém com velocidade constante. Considere a posição da frente do trem quando o engenheiro aciona os freios.
As vacas por perto vão testemunhar uma colisão?
Questão 77
O engenheiro de um trem de passeio, viajando a , avista um vagão de carga adiante na mesma via (Figura abaixo). O vagão de carga viaja a na mesma direção que o trem de passeio. O engenheiro do trem freia imediatamente, com uma aceleração constante de , enquanto o vagão de carga se mantém com velocidade constante. Considere a posição da frente do trem quando o engenheiro aciona os freios.
Em um único gráfico, esboce as posições da frente do trem e do fim do vagão
Ver solução completaQuestão 78
Se um móvel percorre uma determinada trajetória com aceleração e velocidade positivas, podemos afirmar que o tipo de movimento uniformemente variado percorrido pelo móvel neste caso é:
(a) retrógrado e acelerado
(b) progressivo e retardado
(c) progressivo e acelerado
(d) circular e acelerado
(e) retrógrado e retardado
Ver solução completaQuestão 79
3) Um cachorro avista um pote de flores passar subindo e depois descendo por uma janela de de altura. O tempo total em que o pote é visto é de . Determine a altura alcançada pelo pote acima da janela
Ver solução completaQuestão 80
2) Um paraquedista, depois de pular, cai sem atrito. Quando o paraquedas abra ele desacelera a e alcança o solo à velocidade de .
a) Quanto tempo o paraquedista permanece no ar?
b) A que altura começou a queda.
Ver solução completaQuestão 81
5) Uma partícula sobre três deslocamentos sucessivos em um plano da seguinte forma: para sudoeste, para leste e para a direção ao norte de leste. Escolhendo o eixo orientado para leste e o eixo orientado para norte, determine
a) As componentes de cada deslocamento,
b) As componentes do deslocamento resultante,
c) o módulo e a direção do deslocamento resultante,
d) o deslocamento requirido para trazer a partícula retornar ao ponto de partida
Ver solução completaQuestão 82
(Capítulo 2.7 – Exercício 30) Os freios de um carro podem produzir uma desaceleração da ordem de . (a) Se o motorista está a e avista um policial rodoviário, qual é o tempo mínimo necessário para que o carro atinja a velocidade máxima permitida de ? (A resposta revela a inutilidade de frear para tentar impedir que a alta velocidade seja detectada por um radar ou por uma pistola de laser.) (b) Desenhe os gráficos de em função de e em função de durante a desaceleração.
Ver solução completaQuestão 83
4) Um elevador sobe com movimento retilíneo uniforme. Uma pessoa está dentro deste elevador em repouso em relação a ele. Sobre esta pessoa atuam a força peso e a força normal De acordo com a terceira lei de Newton, indique onde é aplicada a força de reação a e a , respectivamente.
(a) Na própria pessoa e na própria pessoa
(b) No centro da Terra e no piso do elevador
(c) Na própria pessoa e no piso do elevador
(d) No centro da Terra e na própria pessoa
(e) No piso do elevador e no piso do elevador
Ver solução completaQuestão 84
8) Considere um objeto que se move ao longo do eixo cuja posição inicial é . O gráfico velocidade tempo deste movimento está representado abaixo.
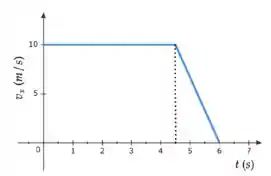
São realizadas as seguintes afirmativas:
- A posição em é de
- A distância percorrida entre os instantes e é de 40m;
- A velocidade em é nula.
São verdadeiras:
- Apenas a I
- Apenas a II
- Apenas III
- Todas
- Nenhuma
Questão 85
Ignorando a resistência do ar em gotas de chuva, podemos considerar as gotas como objetos em queda livre.
Calcule (baseado nas suas observações pessoais da chuva) a velocidade que as gotas realmente atingem o solo.
Ver solução completaQuestão 86
Do topo de um prédio, um estudante arremessa um balão d’água verticalmente para baixo. O balão deixa a mão dele com velocidade igual a Desconsidere a resistência do ar para que o balão esteja em queda livre assim que abandona a mão do estudante.
Qual a velocidade depois de de queda?
Ver solução completaQuestão 87
Ignorando a resistência do ar em gotas de chuva, podemos considerar as gotas como objetos em queda livre.
A partir das suas respostas para e , a estimativa obtida ao se ignorar a resistência do ar é boa? Explique.
Ver solução completaQuestão 88
Quais dos objetos descritos abaixo pode ser considerado um referencial inercial ?
(a) Um objeto em um movimento circular com aceleração tangencial constante
(b) Um objeto em um movimento circular uniforme;
(c) Um objeto em um movimento retilíneo uniforme;
(d) Um objeto em um movimento retilíneo uniformemente variado;
(e) Um objeto em um movimento retilíneo com aceleração que varia no tempo;
Ver solução completaQuestão 89
Um objeto movendo-se ao longo de uma linha reta pode ter rapidez crescente com módulo da aceleração decrescente?
(A) Não, isso é impossível por causa da definição de aceleração.
(B) Não, porque se o módulo da aceleração diminuir o objeto se moverá cada vez mais devagar.
(C) Sim, um exemplo seria um objeto caindo verticalmente sem resistência do ar.
(D) Sim, um exemplo seria um objeto caindo verticalmente a partir do repouso com resistência do ar.
(E) Sim, um exemplo seria um objeto subindo verticalmente sem resistência do ar.
Ver solução completaQuestão 90
Considere dois corpos de mesma forma e mesmo volume, mas com massas diferentes. Considere, ainda, que para uma determinada forma, a resistência do ar só depende da velocidade, sendo sempre oposta a ela e aumenta linearmente com ela. Quando caem de uma altura suficientemente grande, partindo do repouso, em determinado momento passarão a ter velocidade constante.
Ver solução completaQuestão 92
Um motorista possui tempo de reação de , e a desaceleração máxima que seu carro atinge é de . Ele está dirigindo na estrada a quando, subitamente, vê um obstáculo a à frente. Ele consiguirá parar o carro e evitar uma colisão?
Ver solução completaQuestão 93
No instante um carro tem velocidade de . Ele reduz sua velocidade com uma aceleração dada por ( em e em ). Ele para no instante:
Questão 94
Um veículo parte do repouso em movimento retilíneo e acelera a . Pode-se dizer que sua velocidade e a distância percorrida, após segundos, valem, respectivamente:
(a) 6 m/s e 18 m;
(b) 6 m/s e 12 m;
(c) 3 m/s e 9 m;
(d) 3 m/s e 6 m;
(e) 6 m/s e 9 m;
Ver solução completaQuestão 95
Um móvel parte da origem do movimento com velocidade e aceleração durante . Em seguida mantém-se em velocidade constante durante . Logo após o móvel começa a reduzir sua velocidade a uma taxa de até parar.
A) qual o deslocamento total do móvel.
B) qual a velocidade média do móvel durante o deslocamento.
OBS: Efetue o arredondamento em 1 (uma) casa decimal.
Ver solução completaQuestão 96
Se já nem sei o meu nome
Se eu já não sei parar
Viajar é mais, eu vejo mais
A rua, luz, estrada, pó
O jipe amarelou.
Trecho da música Manuel, o Audaz de Toninho Horta.
Os versos da música, citados acima, descrevem a emoção de uma viajem. Em uma viajem de jipe, nos movemos e paramos e depois nos movemos de novo. Tudo para ter o prazer de conhecer novos lugares.
Em um desses momentos de variação de velocidade, podemos dizer, que o jipe executa a seguinte equação horária da velocidade: . Esse movimento pode ser descrito como:
(a) Movimento Retilíneo Uniforme retardado, onde a velocidade inicial se dá no sentido do movimento.
(b) Movimento Retilíneo Uniforme acelerado, onde a velocidade inicial se dá no sentido contrário do movimento.
(c) Movimento Retilíneo Uniforme acelerado, onde a velocidade inicial se dá no sentido do movimento.
(d) Movimento Retilíneo Uniforme retardado, onde a velocidade inicial se dá no sentido contrário do movimento.
(e) Movimento Retilíneo Uniforme acelerado, onde a velocidade inicial se dá à 3m/s do início da trajetória.
Ver solução completaQuestão 97
Do alto de uma torre de de altura, uma esfera e lançada com velocidade de numa direção que forma com a horizontal, para baixo. Desconsiderando a resistência do ar e admitindo , , qual o instante e a distância que a esfera atinge o solo, respectivamente?
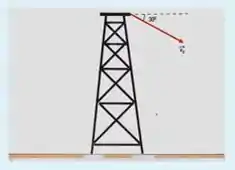
Escolha uma opção:
- e
- e
- e
- e
- e
- e
- e
Questão 98
Na célebre corrida entre a lebre e a tartaruga, a velocidade da lebre é de e a da tartaruga de . A distância total a percorrer é de em linha reta. Depois de a lebre para e tira uma soneca de minutos, e depois acorda e continua com a mesma velocidade anterior de . Deixe todas as respostas em unidades do SI.
Em quais instantes a tartaruga e a lebre se cruzam? Quais as posições delas nesses instantes?
Ver solução completaQuestão 99
Um engenheiro está projetando uma pista de aeroporto. Os aviões que usarão tal pista podem acelerar a uma taxa de . Para uma decolagem segura o avião deve estar a uma velocidade maior que . Qual é, aproximadamente, o comprimento mínimo da pista?
a)
b)
c)
d)
e)
Ver solução completaQuestão 101
Enunciado das questões Q1 e Q2
Uma partícula move-se em um plano horizontal com velocidade constante . Ao passar pelo ponto de coordenadas , no instante , ela passa a sofrer uma aceleração constante .
Q1
Em que instante a partícula passa por ? Dê sua resposta em segundos.
a) 2,0
b) 3,0
c) 4,0
d) 5,0
e) 6,0
Ver solução completaQuestão 102
Enunciado das questões Q1 e Q2
Uma partícula move-se em um plano horizontal com velocidade constante . Ao passar pelo ponto de coordenadas , no instante , ela passa a sofrer uma aceleração constante .
Q2
Qual é a distância que a partícula está em relação à origem do sistema de coordenadas, quando ? Dê sua resposta em metros.
a) 40
b) 50
c) 60
d) 70
e) 80
Ver solução completa