Deslocamento vetorial
Produzido por Ludovic BeghinTeoria
Fala aí, você acaba de chegar no Responde Aí. Vamos aprender hoje sobre o deslocamento vetorial.
Deslocamento
Quando a gente começa a aprender o movimento dos corpos na física, uma das primeiras coisas que vemos é o deslocamento do corpo, que era dado pela diferença entre a posição final e a posição inicial:
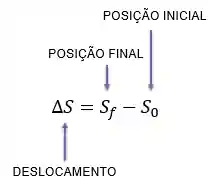
Tudo lindo até aí, então para que eu tenho que saber o vetor deslocamento? Sempre que coloca vetor fica ruim, né? hahaha
A grande questão é que a grandeza deslocamento escalar funciona muito bem para o movimento em uma única dimensão, mas quando queremos estudar o movimento em duas ou mais direções, ou seja, haverá deslocamento na direção
Deslocamento Vetorial
Mas fica tranquilo, não muda muita coisa não. O deslocamento vetorial (ou vetor deslocamento) também é uma diferença entre posição final e inicial, mas agora consideramos o vetor posição final menos vetor posição inicial:
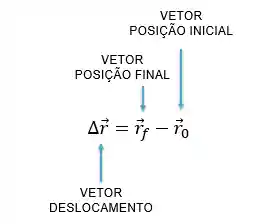
Representação por vetores unitários
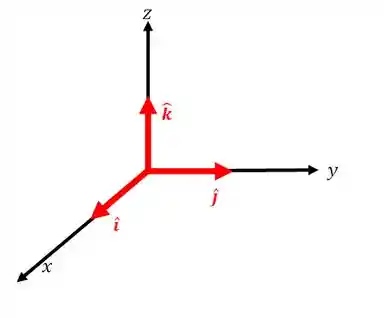
Quando estamos estudando física, mecânica e movimento, a melhor forma de representar vetores é usando os vetores unitários.
É bem simples, pra cada um dos três eixos
Módulo do deslocamento vetorial
Uma coisa que costuma pedir nas questões é a distância absoluta entre as posições finais e iniciais e isso a gente encontra fazendo o módulo do vetor deslocamento.
Se nós temos um vetor deslocamento:
Para obter o módulo fazemos o seguinte:
Exemplo
Uma bola é deslocada do ponto
a) Qual é o deslocamento vetorial?
b) Qual o módulo do deslocamento vetorial?
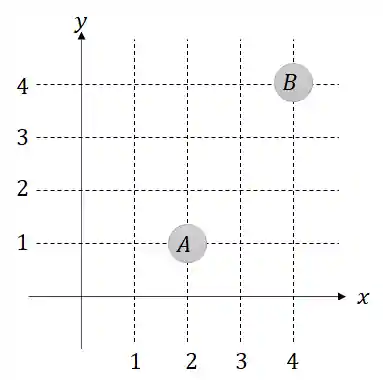
Passo 1: Encontrar o vetor posição inicial e o vetor posição final
Os vetores posição inicial e final são os vetores que começam na origem do plano cartesiano e terminam no ponto
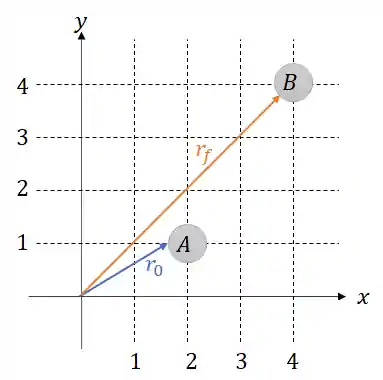
Passo 2: Calculando o deslocamento vetorial
Uma vez que temos os vetores de posição inicial e final, vamos aplicar a fórmula para encontrar o vetor deslocamento:
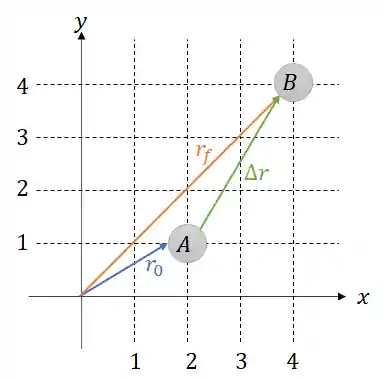
Logo
E prontinho, temos o deslocamento vetorial.
Passo 3: Calcular o deslocamento vetorial.
Agora que a gente tem o deslocamento vetorial, podemos calcular o módulo desse vetor e descobrir o valor absoluto do deslocamento:
Videoaula
Pra ficar ainda mais ligado, dá uma olhada nessa videoaula
É isso que temos para esse tópico! Bora para os exercícios para fixar isso melhor? 👇
Deslocamento Vetorial
Módulo do deslocamento vetorial
Exemplo
Videoaula
Exercícios Resolvidos
Exercício Resolvido #1
UFPB
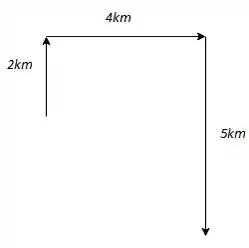
Um cidadão está à procura de uma festa. Ele parte de uma praça, com a informação de que o endereço estaria situado a 2km ao norte. Após chegar ao referido local, ele recebe nova informação de que deveria se deslocar 4km para leste. Não encontrando ainda o endereço, o cidadão pede informação a outra pessoa, que diz estar a festa acontecendo a 5km ao sul daquele ponto. seguindo essa dica, ele finalmente chega ao evento. Na situação descrita, o modulo do veto deslocamento do cidadão, da praça até o destino final, é?
a) 11kmb) 7km
c) 5km d) 4kme) 3km
Passo 1
Bom, o primeiro passo é a gente desenhar os vetorzinhos que a questão tá descrevendo pra gente! Então bora lá, a gente fica com algo desse jeito:
Sacou? Então nosso deslocamento resultante é só a gente ligar o ponto inicial ao ponto final, tranquilo? Bora lá:
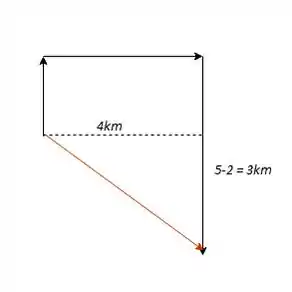
Massa! Então agora é só a gente fazer pitágoras e calcular a hipotenusa desse triângulo, que é exatamente o nosso vetor resultante! Então temos:
Showwww!
Resposta
c) 5km
Exercício Resolvido #2
UFC-CE
Analisando a disposição dos vetores BA, EA, CB, CD e DE, conforme figura a seguir, assinale a alternativa que contém a relação vetorial correta:
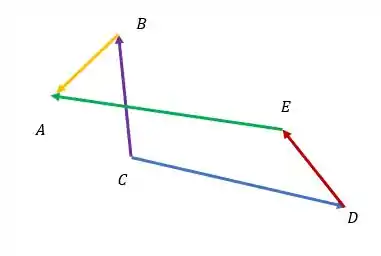
a) CB + CD + DE = BA + EA
b) BA + EA + CB = DE + CD
c) EA – DE + CB = BA + CD
d) EA – CB + DE = BA – CD
e) BA – DE – CB = EA + CD
Passo 1
Pra gente resolver essa parada vamos analisar o caminho percorrido pra chegar de um ponto ao outro e após isso analisar quais caminhos são iguais.
Por exemplo, temos dois jeitos de sair de para .
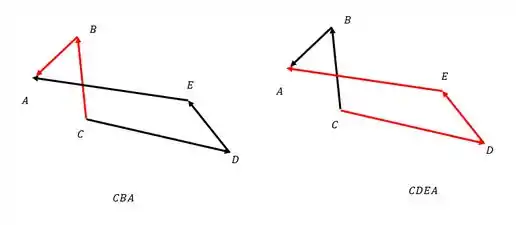
Podemos fazer o percurso ou o percurso e em ambos os percursos o deslocamento resultante será de para .
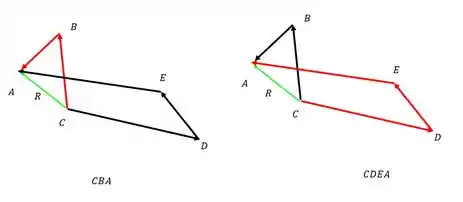
É como quando pegamos um caminho mais longo pra chegar no mesmo local, mesmo que o percurso seja maior o resultado final é o mesmo pois acabamos andando no sentido oposto do que se queria chegar.
Passo 2
Conhecendo agora que esses percursos são iguais pois saem do mesmo ponto e chegam num mesmo ponto, podemos escrever isso do jeito que a questão nos pede.
Putz mas não tem essa resposta lá, e agora?

Fica tranquilo, essa resposta tem lá sim só que não tá no formato certo das alternativas, vamos analisar.
a) CB + CD + DE = BA + EA
b) BA + EA + CB = DE + CD
c) EA – DE + CB = BA + CD
d) EA – CB + DE = BA – CD
e) BA – DE – CB = EA + CD
Temos que ter aqui e com sinais opostos isso não ocorre na alternativa b nem c e nem na alternativa e, sobrando só pra gente as alternativas a e d. Olhando pra alternativa a temos e no mesmo lado com mesmo sinal, o que não acontece na nossa igualdade.
Nossa vencedora então é a alternativa d, e pra chegarmos nela é só passar pra um lado e pro outro.
E trocar os lados né já que essa alternativa maluca inverteu tudo pra confundir ainda mais a nossa cabeça.
Resposta
Exercício Resolvido #3
PUCCAMP SP
Num bairro onde todos os quarteirões são quadrados e as ruas paralelas distam 100m uma da outra, um transeunte faz o percurso de P a Q pela trajetória representada no esquema:
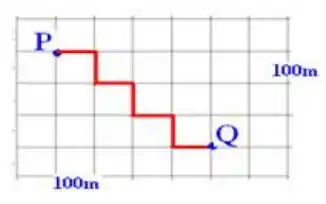
O deslocamento vetorial desse transeunte tem módulo, e metros, igual a:
- 300
- 350
- 400
- 500
- 700
Passo 1
Como a gente sabe, o vetor deslocamento é só calcularmos o módulo da distância do ponto inicial até o ponto final, sacou? Então temos o seguinte triângulo:
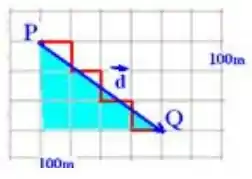
Com catetos de 3 e 4 quadradinhos. Como cada um vale 100m, é só usarmos pitágoras pra encontrar a hipotenusa, que vale 500m, e é igual ao nosso vetor deslocamento! Show! :D
Resposta
d) 500
Exercício Resolvido #4
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 1 , 8º ed. Rio de Janeiro: LTC , 2008, pp 84-2
Uma semente de melancia possui as seguintes coordenadas: e . Determine o vetor posição da semente na notação de vetores unitários e como um módulo e um ângulo em relação ao sentido positivo do eixo . Desenhe o vetor em um sistema de coordenadas dextrogiro. Se a semente é transportada até as coordenadas determine seu deslocamento na notação de vetores unitários e como um módulo e um ângulo em relação ao sentido positivo do eixo .
Passo 1
A notação de vetor unitário, basta colocar as coordenadas para representar os eixos respectivamente.
no início a semente de melancia possuía as coordenadas , e que vão ser as posição
, e do vetor
Então o vetor posição fica:
Passo 2
Vamos fazer o módulo de
Substituindo os valores temos:
Passo 3
Para achar o ângulo entre dois vetores, vimos uma fórmula, como queremos encontrar o ângulo entre o vetor e o eixo positivo, vamos encontrar o ângulo do vetor com um vetor que esteja na direção do positivo.
Então vamos achar o vetor que representa o sentido positivo do eixo , que é o vetor unitário , onde :
De módulo 1
Assim podemos aplicar a fórmula do ângulo entre dois vetores
Já temos os módulos dos dois vetores, basta acharmos o valor do produto escalar entre eles e calcularemos esse valor por essa fórmula
Substituindo todos os valores encontrado na equação do ângulo temos
Passo 4
Primeiro, o que é um sistema de coordenadas dextrogiro??
É simplesmente isso:
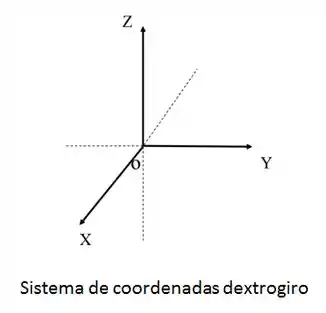
Como as coordenadas no eixo são zero, podemos para simplificar o desenho desenhar em duas dimensões
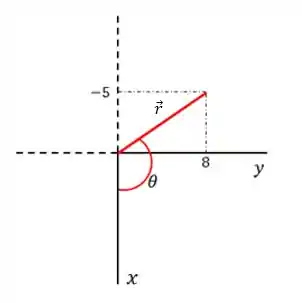
O ângulo theta do desenho é o ângulo encontrado anteriormente .
Passo 5
O vetor deslocamento é dado por
Substituindo a posição inicial e a final teremos
Passo 6
O modulo de é
Passo 7
Como fizemos no item vamos primeiro achar o produto escalar entre e
Assim podemos aplicar a fórmula do ângulo entre dois vetores
Substituindo todos os valores na equação do ângulo temos
Resposta
Exercício Resolvido #5
UFRN
Uma característica da profissão de carteiro é que ele anda muito através das ruas, fazendo diversos percursos ao longo do seu dia de trabalho. Considere a situação do mapa representado pela figura abaixo, na qual um carteiro que se encontra no ponto A, localizado na Av. Amintas Barros, se desloca 400m até atingir o cruzamento desta com a Av. Xavier da Silveira, ambas as avenidas situadas em Natal.
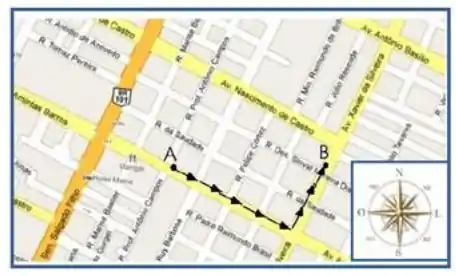
Em seguida, a partir daquele cruzamento, o carteiro se desloca por mais 300m nesta última avenida até chegar ao endereço procurado, localizado no ponto B.
Considerando o percurso e as orientações indicadas no mapa, pode-se afirmar que o módulo, a direção e o sentido do vetor deslocamento do carteiro são, respectivamente,
a) 700m, L-O e para L.
b) 500m, O-L e para O.
c) 500m, O-L e para L.
d) 700m, L-O e para O.
Passo 1
Pra gente encontrar o vetor deslocamento vamos fazer a resultante desses dois vetores, traçando uma reta entre os pontos e formando um triângulo.
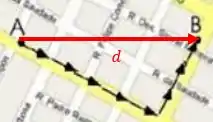
Agora pra gente encontrar a distância é só aplicar o teorema de Pitágoras, já que temos um triângulo retângulo.
Passo 2
Para encontrar a direção e o sentido vamos analisar o percurso do carteiro usando a rosa dos ventos mostrada no enunciado.
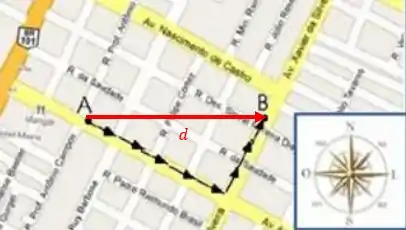
A direção a gente pode dizer que é de onde viemos para onde vamos, na definição matemática é o eixo cartesiano. No caso aqui o carteiro começa no oeste e vai para leste então a direção é o eixo desse deslocamento.
O sentido é como se disséssemos “está no sentido positivo do eixo . Se a gente analisar essa rosa dos ventos como um eixo cartesiano poderíamos dizer que leste é o sentido positivo do eixo .
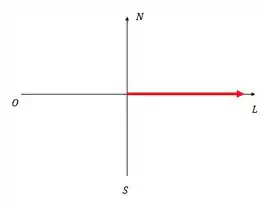
Então o carteiro está no sentido leste
Sendo assim a resposta é: c) 500m, e para .
Resposta
c) 500m, e para .
Exercício Resolvido #6
Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp 27 - Modificado
Uma velejadora encontra ventos que impelem seu pequeno barco a vela. Ela veleja de oeste para leste, a seguir para sudeste e depois uma certa distância em direção desconhecida. No final do trajeto ela se encontra a diretamente a leste de seu ponto de partida como a figura abaixo. Determine o modulo, a direção e o sentido do terceiro deslocamento.
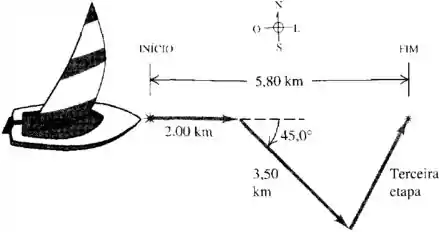
Passo 1
Precisamos achar os componentes da terceira etapa. Vamos primeiro achar os deslocamentos vetoriais da primeira e segunda etapa.
Na primeira etapa vamos ter só movimento na horizontal
Passo 2
Para a segunda etapa devemos decompor o deslocamento usando a “regra do COlado/SEparado”
Escrevendo vetorialmente
Passo 3
O enunciado diz que ele voltou na direção leste , dessa forma podemos ver que a soma dos três vetores deve resultar em um vetor indo para leste :
Passo 4
Escrever na forma vetorial já diz a direção e sentido, precisamos agora achar seu módulo
Resposta
Exercício Resolvido #7
Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp 27 - Modificado
Um esquiador percorre com ângulo de considerando rotação em sentido do sul para o oeste, a seguir a em sentido do leste para o norte, e finalmente a em sentido do oeste para o sul. Qual a distância entre o início e fim do trajeto.
Dados:
Passo 1
Para calcular a distância entre o início e o final devemos achar o deslocamento vetorial desse esquiador. Vamos considerar o início saindo da origem.
Primeiro ele percorre com ângulo de considerando rotação em sentido do sul para o oeste. Vamos ver uma figura para ver como isso fica.
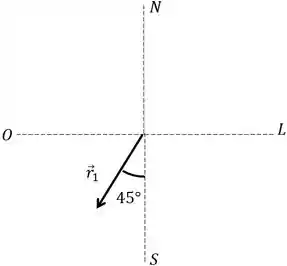
Passo 2
Vamos achar agora suas componentes usando a “regra do COlado/SEparado”
O deslocamento fica
Passo 3
Vamos agora achar o segundo deslocamento, fazendo de novo uma figura para ajudar.
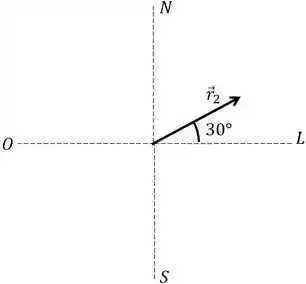
Vamos achar agora suas componentes usando a “regra do COlado/SEparado”
O deslocamento fica
Passo 4
Vamos agora achar o terceiro trecho.
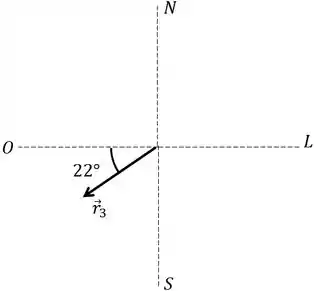
Vamos achar agora suas componentes usando a “regra do COlado/SEparado”
O deslocamento fica
Passo 5
O total vai ser
Passo 6
A distância entre o início e o fim é o módulo do vetor deslocamento total.
Resposta
Exercício Resolvido #8
Paul A. Tipler e Gene Mosca, Física Para Cientistas e Engenheiros, Volume 1, 6ª edição, Cap 3, pp 85-42.
Um explorador caminha para leste, a partir do acampamento, vira então para a esquerda e caminha sobre um arco de círculo centrado no acampamento e, finalmente, caminha mais direto para o acampamento. A que distância o explorador está do acampamento ao fim dessa caminhada? Qual a orientação da posição do explorador em relação ao acampamento? Qual é a razão entre a magnitude final do deslocamento e a distância total caminhada?
Passo 1
O primeiro passo é desenhar grosseiramente o movimento que o explorador fez, para conseguirmos analisar melhor o movimento que ele fez.
O movimento deve ser algo parecido com isso
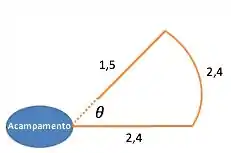
Passo 2
Resolver esse item é necessário ter uma “sacada” não muito trivial.
Ao final de andar os primeiros para leste o explorador começa a caminhar sobre um arco de círculo centrado no acampamento.
Se o centro do círculo é o acampamento, não importa se ele andou sobre o círculo ou , quando ele parar de andar, sua distância em relação ao acampamento será a mesma de quando ele começou, pois será o raio do círculo, que foi determinado pelos primeiros andados.
Então quando ele termina de andar os sobre o círculo centrado no acampamento, ele está a do acampamento. Como o explorador anda diretamente para o acampamento, significa que sua distância para o acampamento é:
Passo 3
Para sabermos a orientação do explorador, precisamos saber quantos graus equivalem aos andados sobre o círculo. Para assim sabermos em qual posição o explorador parou.
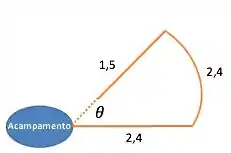
Vamos fazer uma regra de três para descobrir o valor do ângulo.
Sabemos que equivale a , assim:
Temos que o vetor posição do explorador está a acima do eixo leste.
Passo 4
O deslocamento já calculamos e vimos que , a distância percorrida é a soma dos quando ele andou e por isso temos :
Fazendo a Razão do deslocamento final, com a distância percorrida, chegamos em:
Resposta
O vetor posição do explorador está a acima do eixo leste.