Exercícios de Vetor Deslocamento - Lista de Exercícios Resolvida

Uma característica da profissão de carteiro é que ele anda muito através das ruas, fazendo diversos percursos ao longo do seu dia de trabalho. Considere a situação do mapa representado pela figura abaixo, na qual um carteiro que se encontra no ponto A, localizado na Av. Amintas Barros, se desloca 400m até atingir o cruzamento desta com a Av. Xavier da Silveira, ambas as avenidas situadas em Natal.

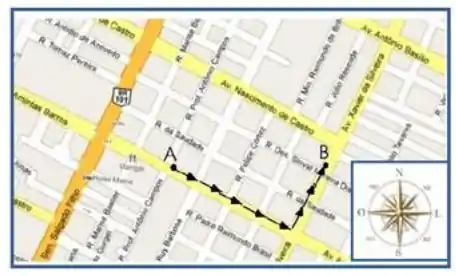
Em seguida, a partir daquele cruzamento, o carteiro se desloca por mais 300m nesta última avenida até chegar ao endereço procurado, localizado no ponto B.

Considerando o percurso e as orientações indicadas no mapa, pode-se afirmar que o módulo, a direção e o sentido do vetor deslocamento do carteiro são, respectivamente,

a) 700m, L-O e para L.           

b) 500m, O-L e para O.           

c) 500m, O-L e para L.           

d) 700m, L-O e para O.

Um cidadão está à procura de uma festa. Ele parte de uma praça, com a informação de que o endereço estaria situado a 2km ao norte. Após chegar ao referido local, ele recebe nova informação de que deveria se deslocar 4km para leste. Não encontrando ainda o endereço, o cidadão pede informação a outra pessoa, que diz estar a festa acontecendo a 5km ao sul daquele ponto. seguindo essa dica, ele finalmente chega ao evento. Na situação descrita, o modulo do veto deslocamento do cidadão, da praça até o destino final, é?

a) 11kmb) 7km

c) 5km d) 4kme) 3km

Analisando a disposição dos vetores BA, EA, CB, CD e DE, conforme figura a seguir, assinale a alternativa que contém a relação vetorial correta:

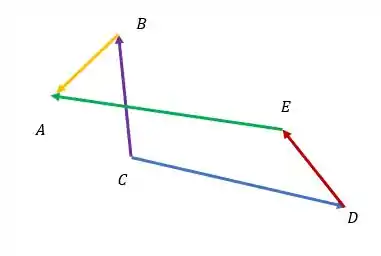
a) CB + CD + DE = BA + EA                             

b) BA + EA + CB = DE + CD                                

c) EA – DE + CB = BA + CD     

d) EA – CB + DE = BA – CD                           

e) BA – DE – CB = EA + CD

Num bairro onde todos os quarteirões são quadrados e as ruas paralelas distam 100m uma da outra, um transeunte faz o percurso de P a Q pela trajetória representada no esquema:

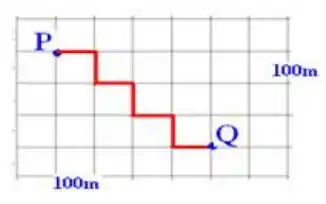
O deslocamento vetorial desse transeunte tem módulo, e metros, igual a:

1. 300
2. 350
3. 400
4. 500
5. 700

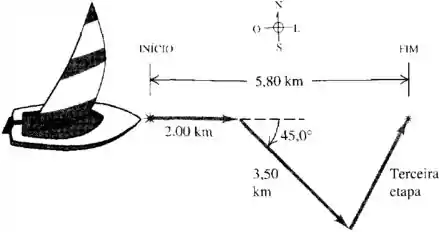
Uma velejadora encontra ventos que impelem seu pequeno barco a vela. Ela veleja de oeste para leste, a seguir para sudeste e depois uma certa distância em direção desconhecida. No final do trajeto ela se encontra a diretamente a leste de seu ponto de partida como a figura abaixo. Determine o modulo, a direção e o sentido do terceiro deslocamento.

Um explorador caminha para leste, a partir do acampamento, vira então para a esquerda e caminha sobre um arco de círculo centrado no acampamento e, finalmente, caminha mais direto para o acampamento. A que distância o explorador está do acampamento ao fim dessa caminhada? Qual a orientação da posição do explorador em relação ao acampamento? Qual é a razão entre a magnitude final do deslocamento e a distância total caminhada?

Um esquiador percorre com ângulo de considerando rotação em sentido do sul para o oeste, a seguir a em sentido do leste para o norte, e finalmente a em sentido do oeste para o sul. Qual a distância entre o início e fim do trajeto.

Dados:

Uma semente de melancia possui as seguintes coordenadas: e . Determine o vetor posição da semente na notação de vetores unitários e como um módulo e um ângulo em relação ao sentido positivo do eixo . Desenhe o vetor em um sistema de coordenadas dextrogiro. Se a semente é transportada até as coordenadas determine seu deslocamento na notação de vetores unitários e como um módulo e um ângulo em relação ao sentido positivo do eixo .

Dois carros e (considerados como partículas) partem da mesma posição no instante e percorrem estradas perpendiculares, seguindo para o norte e o leste, respectivamente, com velocidades contantes e . A distância entre os dois carros no instante satisfaz à relação:

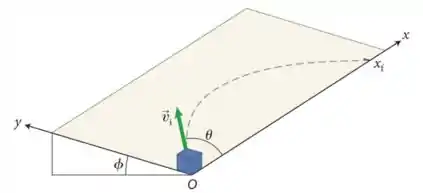
Um bloco de inércia está localizado na origem de um sistema de coordenadas alinhado em relação a um plano inclinado que faz um ângulo em relação a horizontal (ver a figura abaixo). Você lança um bloco ao longo da inclinação, com velocidade inicial fazendo um ângulo com o eixo do plano inclinado.

a) Qual é o módulo e a direção da aceleração do bloco expressa no sistema de coordenadas indicado na figura?

b) Derive a expressão para a velocidade do bloco em função do tempo, expressa em notação vetorial para o sistema de coordenadas indicado.

c) Qual é o valor máximo do deslocamento do bloco, , ao longo do eixo ?

d) Qual é o máximo deslocamento do bloco, , ao longo do eixo . Ignore o atrito e qualquer outra dissipação.

e) Discuta seus resultados nas situações extremas e

Um trenó e seu ocupante, com uma massa total de 85 kg, descem uma encosta e atingem

um trecho horizontal retilíneo com uma velocidade inicial de . Se uma força desacelera o trenó até o repouso a uma taxa constante de

1. Qual é o módulo dessa força F?
2. Que distância o trenó percorre até parar?
3. Qual o trabalho realizado pela força F sobre o trenó?

Um pequeno esquilo atravessa um jardim, deslocando-se segundo as coordenadas e , sendo e dimensionados e em metros e em segundos. No instante , o vetor posição em termos de vetores unitários que descreve o movimento do esquilo é igual a:

a)

b)

c)

d)

e)

O trem sai de uma estação a partir do repouso, rumo ao oeste, com aceleração constante de . Já o trem se move do norte para o sul com velocidade constante de , e passa por essa mesma estação segundos após a partida do trem . Considere o versos apontando para leste e o versor para o norte. Considere também a estação na origem do sistema de coordenadas, e considere o tempo inicial no instante em que o trem sai da estação.

Escreva uma expressão para o vetor posição de em relação à em função do tempo.

Em um jogo de xadrez ao ar livre, no qual as peças ocupam o centro de quadrados com de lado, um cavalo é movido da seguinte forma: (1) dois quadrados para a frente e um quadrado para a esquerda; (2) um quadrado para frente e três quadrados para a direita; (3) dois quadrados para a frente e um quadrado para a direita. Determine o módulo, com uma casa decimal, em metros (em relação ao sentido “para frente”) do deslocamento total do cavalo após a série de três movimentos.

Um objeto descreve um movimento tridimensional de acordo com o vetor posição

, onde a posição está expressa em metros e o tempo está expresso em segundos. Calcular o vetor deslocamento entre o instantes e .

(a)

(b)

(c)

(d)

(e)

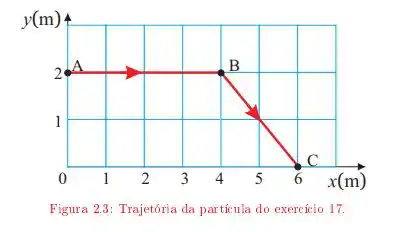
Uma partícula move-se descrevendo a trajetória ABC da figura 2.3 A velocidade da partícula tem módulo constante durante todo o percurso. O início do movimento é em A. Adotando a origem do sistema de referência em 0, determine:

f. O tempo que a partícula leva para sair de A e chegar em C;

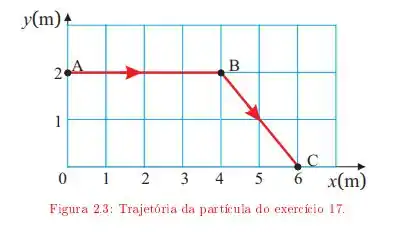
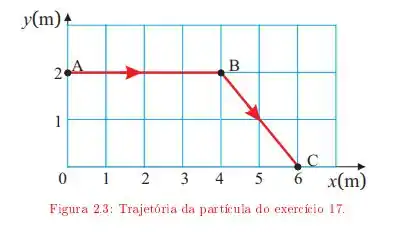
Uma partícula move-se descrevendo a trajetória ABC da figura 2.3 A velocidade da partícula tem módulo constante durante todo o percurso. O início do movimento é em A. Adotando a origem do sistema de referência em 0, determine:

b. O vetor posição em função do tempo, no trecho AB da trajetória;

Uma partícula move-se descrevendo a trajetória ABC da figura 2.3 A velocidade da partícula tem módulo constante durante todo o percurso. O início do movimento é em A. Adotando a origem do sistema de referência em 0, determine:

c. O tempo que a partícula leva para sair de A e chegar em B;

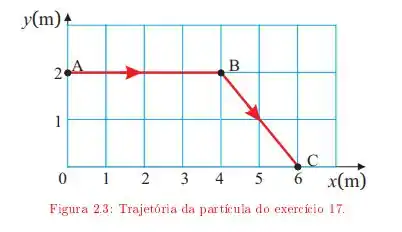
Uma partícula move-se descrevendo a trajetória ABC da figura 2.3 A velocidade da partícula tem módulo constante durante todo o percurso. O início do movimento é em A. Adotando a origem do sistema de referência em 0, determine:

e. O vetor posição em função do tempo, no trecho BC da trajetória;

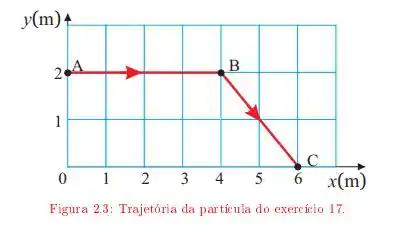
Uma partícula move-se descrevendo a trajetória ABC da figura 2.3 A velocidade da partícula tem módulo constante durante todo o percurso. O início do movimento é em A. Adotando a origem do sistema de referência em 0, determine:

h. A distância total percorrida pela partícula entre os instantes t = 0 e t = 3 s.

Dois objetos A e B iniciam seus movimentos, simultaneamente, nas posições e . Decorridos 5 segundos o corpo A chega em enquanto o corpo B chega em .

a. Qual dos dois corpos teve o maior deslocamento? Calcule e desenhe esses vetores;

Um objeto tem aceleração constante . No instante , a velocidade é zero e o vetor posição é .

a. Determine o vetor velocidade e o vetor posição em função do tempo;

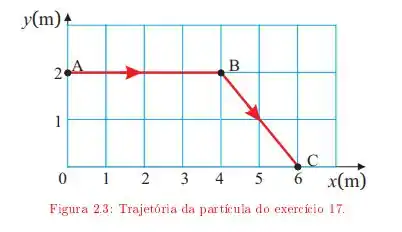
Uma partícula move-se descrevendo a trajetória ABC da figura 2.3 A velocidade da partícula tem módulo constante durante todo o percurso. O início do movimento é em A. Adotando a origem do sistema de referência em 0, determine:

g. O módulo do vetor deslocamento entre A e C;

Um objeto tem aceleração constante . No instante , a velocidade é zero e o vetor posição é .

b. Determine a equação da trajetória no plano xy e faça um desenho desta.

Dois objetos A e B iniciam seus movimentos, simultaneamente, nas posições e . Decorridos segundos o corpo A chega em enquanto o corpo B chega em .

b. Supondo que os deslocamentos foram retilíneos e uniformes, calcule a distância entre os dois corpos, em função do tempo, para o intervalo e a distância entre eles para .

A posição de uma partícula em função do tempo é dado por:

onde está em metros e em segundos.

(b) Qual o período do movimento?

Uma partícula percorre, com velocidade constante e no sentido anti-horário, uma circunferência de raio igual a e completa uma volta em segundos. A partícula passa pelo ponto em . Tomando a origem em , de acordo com a figura , determine:

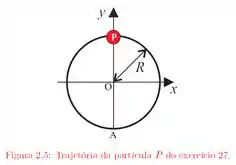
(a) O módulo e a direção dos vetores que descrevem sua posição , e segundos mais tarde;

Uma partícula percorre, com velocidade constante e no sentido anti-horário, uma circunferência de raio igual a e completa uma volta em segundos. A partícula passa pelo ponto em . Tomando a origem em , de acordo com a figura , determine:

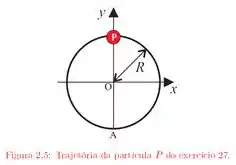
(b) O módulo e a direção do vetor deslocamento no intervalo de tempo de segundos a contar do quinto segundo;

A hélice de um ventilador completa rotações em cada minuto. Considere um ponto localizado na extremidade da hélice que tem um raio de .

(a) Qual a distância percorrida por este ponto em uma volta?

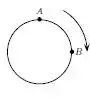
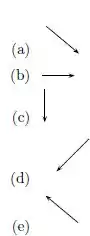
Uma partícula se move, com velocidade de módulo constante, do ponto A para o ponto B, seguindo uma trajetória circular no sentido indicado na figura. O vetor que melhor representa o vetor velocidade média entre estes dois instantes é

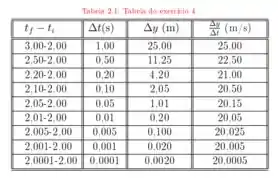
A posição de uma pedra que cai do alto de um rochedo, a partir do repouso, é dada por , medida para baixo a partir da posição inicial .

a. Se é o deslocamento da pedra e a velocidade média, o que você conclui analisando os dados da tabela seguinte?

Se é o vetor posição de uma partícula, cujas coordenadas são dadas em metros e o tempo em segundos, marque qual o valor da coordenada do vetor posição, em metros, quando .

A.

B.

C.

D.

E.

O deslocamento de um corpo é descrito pela equação horária:

Onde o tempo é dado em segundos. O vetor aceleração do corpo é igual a:

(a)

(b)

(c)

(d)

(e)

(f)

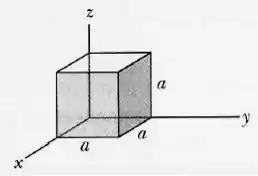
(a) Na Figura abaixo, um cubo de lado a tem um de seus vértices posicionado na origem de um sistema de coordenadas xyz. Uma diagonal de centro é uma linha que vai de um vértice a outro passando pelo centro. Em termos dos vetores unitários, qual é a diagonal de centro que se estende a partir do vértice nas coordenadas (x; y; z) iguais a

(a) (0; 0; 0);

(b) (a; 0; 0);

(c) (0; a; 0),

(d) (a; a; 0)?

(e) Determine os ângulos que as diagonais de centro fazem com os lados adjacentes.

(f) Determine o comprimento das diagonais de centro em função de a.