Campo e Energia em um Capacitor
Produzido por Bruno SoaresTeoria
A Capacitância é a capacidade de um capacitor armazenar carga. Quanto maior for capacitância
Energia Armazenada no Capacitor
Quando armazenamos uma carga no capacitor naturalmente estamos transferindo energia para ele. A energia potencial ou energia armazenada em um capacitor é dada por:
Além disso, como temos que:
Então podemos calcular a energia potencial em função da carga:
Podemos brincar de substituir essa fórmula da energia de outras maneiras, e vamos chegar à três fórmulas diferentes:
📢 Clique para saber mais:
Quer aprender mais sobre a energia em capacitores?! Então bora começar com esse vídeo super completo que o Responde Aí preparou pra você! 😍 👇
Densidade de Energia em Capacitores
Densidade de energia é nada mais nada menos é que a quantidade de energia por unidade de volume. Assim:
Sendo
Vamos trabalhar um pouco mais essa expressão? A gente pode começar abrindo esse volume aí. Visualmente o volume que a gente quer saber aqui é o espaço entre os capacitores, se liga:
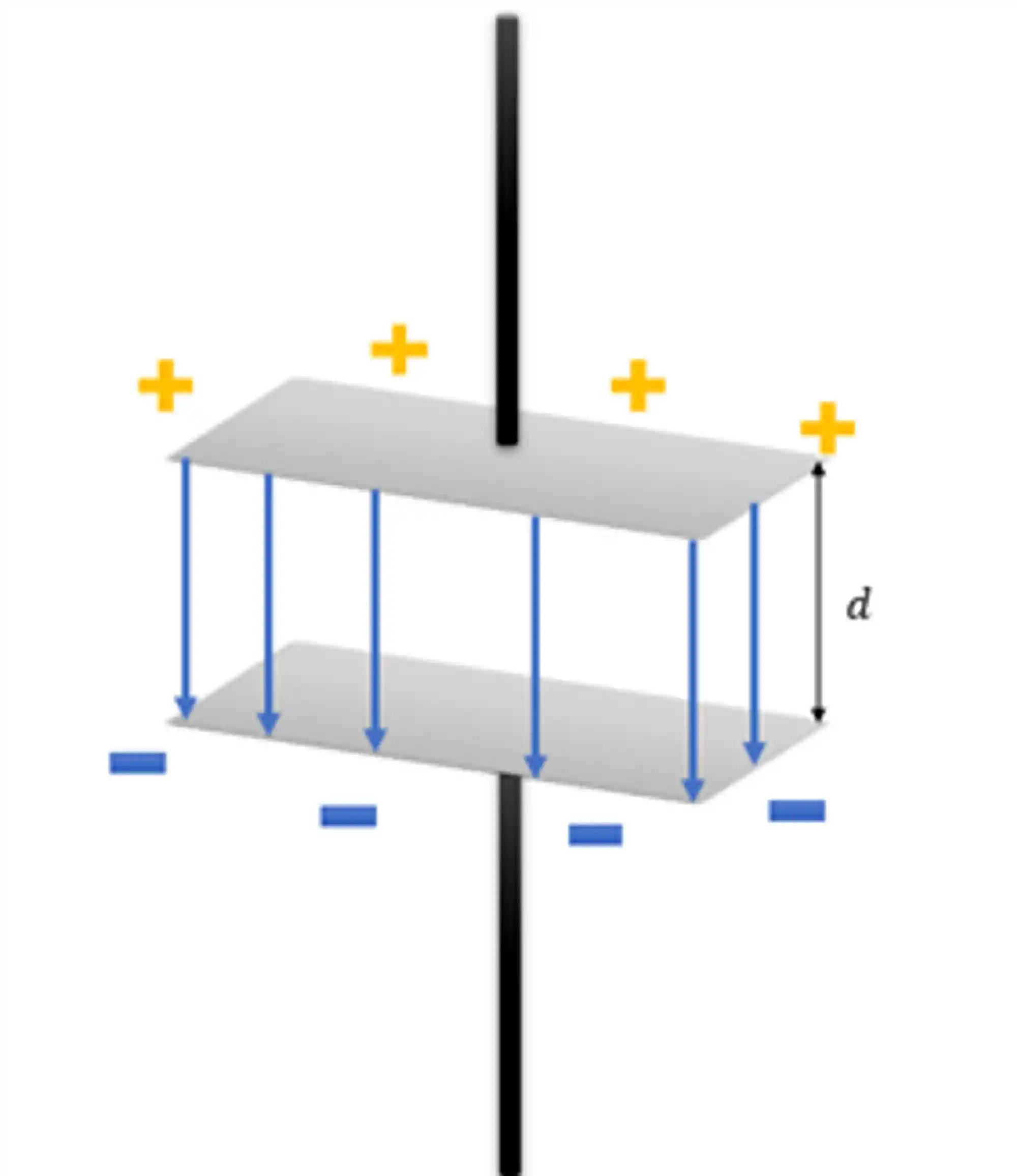
Esse volume da região entre as placas é o produto da área da placa A pela distância entre as placas
Continuando na mesma linha, vamos também substituir na expressão os valores que conhecemos pra voltagem e capacitância.
Substituindo isso tudo na expressão da densidade de energia, teremos:
Essa expressão ainda vai aparecer bastante por aí, mas ela basicamente nos diz que a densidade de energia em um capacitor depende exclusivamente da intensidade do campo elétrico entre suas placas!
Campo Elétrico em Capacitores
Quando carregamos um capacitor criamos um campo elétrico
Onde
Onde
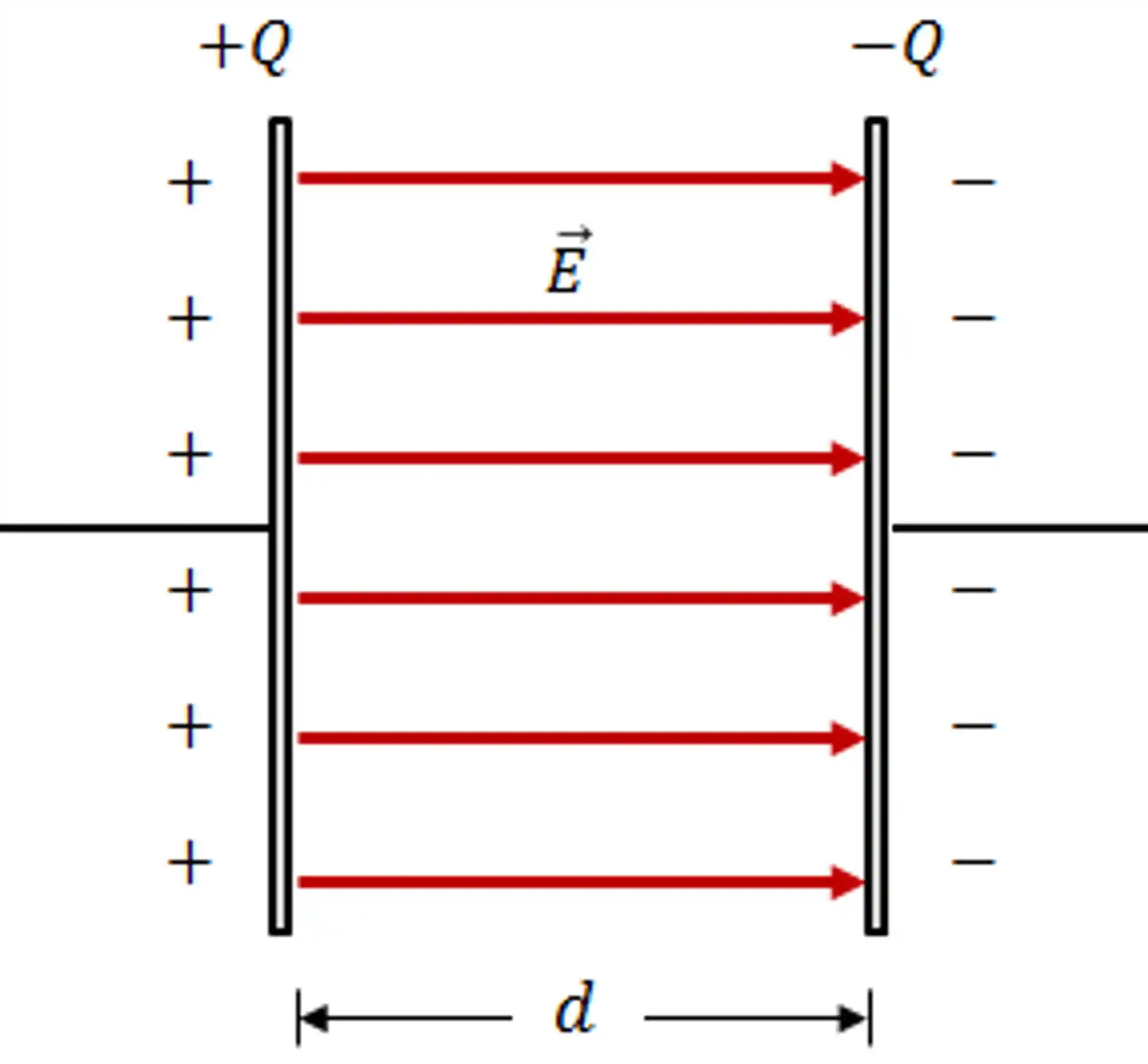
Para cada tipo de capacitor, você substitui os valores de capacitância pra resolver os problemas que vierem!
Exemplo: Um capacitor de placas paralelas possui capacitância C=2μF e carga Q=4μC. Se a distância entre as placas é 1mm encontre o módulo do seu campo elétrico, sua energia e densidade de energia.
O problema esta pedindo pra calcularmos três coisas, a energia no capacitor, seu campo elétrico e a densidade de energia! Vamos começar pelo mais fácil que é a energia no capacitor!
Passo 1: Energia em Capacitores
Para calcular a energia em capacitores usamos a seguinte fórmula:
Substituindo os dados do enunciado:
Passo 2: Módulo do Campo Elétrico do Capacitor
Agora, para calcular o módulo do campo elétrico fazemos:
Todos esses dados foram fornecidos no enunciado, então é só substituir:
Passo 3: Densidade de Energia do Capacitor
Por fim, calculamos a densidade de energia do capacitor com a seguinte fórmula:
Substituindo os dados, temos:
Agora vamos praticar com exercícios?!
Densidade de Energia em Capacitores
Campo Elétrico em Capacitores
Exemplo: Um capacitor de placas paralelas possui capacitância C=2μF e carga Q=4μC. Se a distância entre as placas é 1mm encontre o módulo do seu campo elétrico, sua energia e densidade de energia.
Exercícios Resolvidos
Exercício Resolvido #1
UFRJ-P1-2011.1-Múltipla Escolha n°10.
Qual das seguintes afirmativas é falsa?
- No processo de carregamento de um capacitor, cria-se um campo elétrico entre suas placas.
- O trabalho necessário para se carregar um capacitor pode ser pensado como o trabalho necessário para se criar um campo elétrico entre suas placas
- A densidade de energia na região entre as placas de um capacitor depende linearmente do módulo do campo elétrico
- A diferença de potencial entre as placas de um capacitor plano paralelo depende linearmente do módulo do campo elétrico
- Ao dobrarmos a carga em cada uma das placas de um capacitor dado, dobramos a diferença de potencial entre suas placas
Passo 1
Vamos vendo uma por uma.
No processo de carregamento de um capacitor, cria-se um campo elétrico entre suas placas?
Sim, isso é verdadeiro. Se existe diferença de potencial entre dois pontos (como é o caso das placas opostas do capacitor) então necessariamente existe campo elétrico entre esses dois pontos.
Passo 2
O trabalho necessário para se carregar um capacitor pode ser pensado como o trabalho necessário para se criar um campo elétrico entre suas placas?
Pela mesma lógica do passo 1, isso é verdadeiro.
Passo 3
A densidade de energia na região entre as placas de um capacitor depende linearmente do módulo do campo elétrico?
Falso, basta olhar a fórmula:
Podemos ver que a energia depende linearmente do quadrado do módulo.
Passo 4
A diferença de potencial entre as placas de um capacitor plano paralelo depende linearmente do módulo do campo elétrico?
Verdadeiro, basta olhar a fórmula: . Se não estiver convencido, substitua o campo por um múltiplo dele , você vai ver que o resultado é ter a d.d.p. (diferença de potencial) original multiplicada pelo fator . Por isso a dependência entre o campo e a d.d.p. é linear.
Passo 5
Ao dobrarmos a carga em cada uma das placas de um capacitor dado, dobramos a diferença de potencial entre suas placas?
Verdade pois o campo depende linearmente da carga, por consequência a ddp também depende linearmente dela. Basta ver a Lei de Gauss:
Resposta
Letra c
Exercício Resolvido #2
Elaboração própria.
Um capacitor de é usado em uma câmera fotográfica para armazenar energia. Suponha que o capacitor foi carregado a . Qual é o valor da energia armazenada?
Passo 1
Vimos que a energia em um capacitor é calculada por .
Sabendo que , basta substituirmos os valores certo? :)
Passo 2
A carga vai ser
Então, substituindo na fórmula da energia:
Resposta
Exercício Resolvido #3
UFRJ - 2005
Para a segurança dos clientes, o supermercado utiliza lâmpadas de emergência e rádios transmissores que trabalham com corrente contínua. Para carregar suas baterias, no entanto, esses dispositivos utilizam corrente alternada. Isso é possível graças a seus retificadores que possuem, cada um, dois capacitores de , associados em paralelo. Os capacitores, descarregados e ligados a uma rede elétrica de tensão máxima igual a 170 V, estarão com carga plena após um certo intervalo de tempo t. Considerando t, determine:
a) a carga elétrica total acumulada;
b) a energia potencial total armazenada.
Passo 1
A carga elétrica acumulada é dada por , enquanto a energia potencial será .
Basta substituir os valores :)
Lembrando que, como temos dois capacitores em paralelo precisamos calcular a capacitância equivalente.
Passo 2
a) Calculando a carga total acumulada:
Passo 3
b) A energia potencial vai ser
Resposta
Exercício Resolvido #4
TIPLER, MOSCA, FÍSICA PARA CIENTISTAS E ENGENHEIROS, VOLUME II, 6.ED.
A diferença de potencial entre as placas de um capacitor de é de .
a) Quanta energia é armazenada no capacitor?
b) Quanta energia adicional é necessária para aumentar a diferença de potencial entre as placas de para ?
Passo 1
A energia em um capacitor é calculada por .
Para a letra b, vamos usar a relação para calcular em um de , depois é só substituir na fórmula da energia.
Passo 2
a) A carga aqui vai ser
Então, substituindo na fórmula da energia:
Passo 3
b) Agora, a carga é
Na fórmula de energia:
A energia adicional será a energia necessária quando menos a energia necessária quando . Então:
Resposta
Exercício Resolvido #5
UFRJ-Prova Final-2014.2Múltipla Escolhas n°1.
Um capacitor possui placas paralelas separadas por uma distância igual a . O espaço entre as placas está cheio de poliéster (Constante dielétrica, ), que possui rigidez dielétrica . Qual a voltagem máxima, e a carga máxima possível que o capacitor pode suportar sem que ocorra ruptura dielétrica.
Considere que na ausência do poliéster o capacitor possui capacitância .
;
;
;
;
;
Passo 1
Qual a voltagem máxima.
Entre as placas de um capacitor, o campo elétrico é constante, assim, a voltagem máxima está associada ao campo elétrico máximo por:
Onde é a separação entre as placas, logo:
Passo 2
a carga máxima possível que o capacitor pode suportar sem que ocorra ruptura dielétrica.
A carga máxima está relacionada com a voltagem máxima por:
Onde, por conta do material dielétrico:
Logo:
Substituindo os valores, teremos:
Logo, a resposta certa é a letra .
Resposta
;
Exercício Resolvido #6
UFRJ-P1-2011.1-Discursiva n°2.
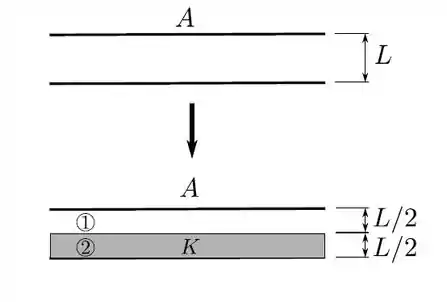
Um capacitor plano-paralelo tem placas idênticas de área , cada uma, com separação entre elas (conforme parte superior da figura ao lado). Numa primeira etapa, tal capacitor é ligado a uma bateria até atingir um módulo de diferença de potencial entre suas placas e, imediatamente, desconectado da bateria.
- Determine o módulo do campo elétrico e a energia eletrostática armazenada
- Determine o módulo da nova diferença de potencial entre as placas.
- Determine o módulo (, , ) do novo campo elétrico em cada uma das duas “metades” ( e ) entre as placas.
- Determine a nova energia eletrostática armazenada .
Numa segunda etapa um isolante de constante dielétrica é inserido no capacitor, preenchendo pela metade região entre suas placas, conforme mostrado na parte inferior da figura ao lado.
Passo 1
a)
Bom, temos a voltagem e a separação entre as placas. O macete é usar a fórmula do potencial:
Só que ele deu o módulo , então vamos trabalhar tudo em módulo:
Como temos que é constante, integramos ao longo do caminho, que é igual ao comprimento do mesmo:
Clássico resultado de capacitores:
Passo 2
Agora podemos aplicar a fórmula da energia armazenada para matar a questão, escolhendo a mais adequada:
A capacitância podemos jogar direto aquela nossa fórmula de bolso:
Passo 3
Como temos duas regiões em série, a voltagem entre elas é a soma das voltagens. Logo:
Podemos achar esses módulos de voltagens integrando o campo, que é uniforme, na região onde estão definidas cada uma delas:
Já o outro, é a mesma integral só que o campo elétrico é dividido pela constante dielétrica:
Somando:
Substituindo o valor da voltagem original :
Passo 4
O campo na primeira região é o mesmo de antes, porque lá não mudou nada.
Na segunda região (onde enfiam um dielétrico) é só dividir pela constante dielétrica:
Passo 5
Para calcular a nova energia armazenada é só substituir na fórmula:
A voltagem nova nós temos... A capacitância nova não... Vamos ter que calcular ela ou tentar outra fórmula. Eu tentaria brincar com essa aqui:
A voltagem nós temos e a carga nova é igual. A carga de dois elementos em série é igual. Logo:
A carga antiga entra na equação relacionando com a capacitância antiga:
Voltando então
E a capacitância antiga nós temos.
E finalmente
Resposta
a)
b)
c)
d)
Exercício Resolvido #7
Site do Prof. A. F. Guimarães, lista 05 de Física 3
Duas placas condutoras quadradas, cada qual com lado igual a , são separadas por uma distância . Uma placa dielétrica com constante dielétrica e com dimensões é inserida até uma distância no espaço entre as placas, como indica a figura.
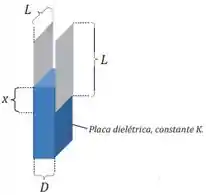
(a) Calcule a capacitância do sistema.
(b) Suponha que o capacitor seja conectado a uma bateria que mantém uma diferença de potencial constante entre as placas. Se a placa dielétrica for inserida até uma distância adicional no espaço entre as placas, mostre que a variação de energia acumulada é dada por:
(c) Suponha que, antes de a placa se mover uma distância , as placas sejam desconectadas da bateria, de modo que as cargas das placas permaneçam constantes. Determine o módulo da carga em cada placa e a seguir mostre que, quando a placa penetra mais uma distância no interior do espaço entre as placas, a energia acumulada varia de uma quantidade igual em módulo, mas de sinal contrário ao valor encontrado no item (b).
Passo 1
(a) Calcule a capacitância do sistema.
Vamos imaginar que o dispositivo da figura seja uma associação de dois capacitores em paralelo, sendo que um deles possui um dielétrico entre suas placas. As capacitâncias para os capacitores sem dielétrico e com dielétrico são dadas por:
Fazendo a associação em paralelos, vamos ter a seguinte capacitância equivalente:
Passo 2
(b) Suponha que o capacitor seja conectado a uma bateria que mantém uma diferença de potencial constante entre as placas. Se a placa dielétrica for inserida até uma distância adicional no espaço entre as placas, mostre que a variação de energia acumulada é dada por:
A energia acumulada no capacitor pode ser calculada como:
Podemos substituir na expressão acima o valor da capacitância equivalente que calculamos. Temos, então:
Podemos agora derivar em relação a para calcular a taxa de variação:
Por fim, temos que:
Passo 3
(c) Suponha que, antes de a placa se mover uma distância , as placas sejam desconectadas da bateria, de modo que as cargas das placas permaneçam constantes. Determine o módulo da carga em cada placa e a seguir mostre que, quando a placa penetra mais uma distância no interior do espaço entre as placas, a energia acumulada varia de uma quantidade igual em módulo, mas de sinal contrário ao valor encontrado no item (b).
A carga acumulada é dada por:
Substituindo o valor de na expressão acima, temos:
Já a energia acumulada é calculada como:
Bem, como queremos calcular a taxa de variação de em relação a , podemos derivar a expressão acima usando a regra da cadeia. Vamos lá:
onde consideramos que a carga é constante! Lembrnado que as placas agora estão desconectadas da bateria ;)
Vamos continuar, agora sim substituindo o valor de na expressão aí de cima:
que é onde queríamos chegar!
Resposta
(a)
(c)
Exercício Resolvido #8
Site do Prof. A. F. Guimarães, lista 05 de Física 3
Seja o capacitor cilíndrico da figura abaixo, com a placa interna carregada com carga negativa , de tal forma que a placa externa tenha a mesma carga, em módulo, porém positiva.
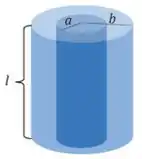
(a) Determine a densidade de energia entre suas placas.
(b) Determine a energia armazenada neste capacitor, usando a relação , onde é um elemento de volume.
Passo 1
(a) Determine a densidade de energia entre suas placas.
Percebemos, inicialmente, que p campo elétrico está orientado de fora para dentro. Podemos usar a lei de Gauss para determinar o módulo do campo elétrico na região entre as placas. Aqui vamos usar uma superfície gaussiana cilíndrica de raio :
Passo 2
A densidade de energia será dada por:
Substituindo o valor de encontrado no Passo 1, temos que:
Passo 3
(b) Determine a energia armazenada neste capacitor, usando a relação , onde é um elemento de volume.
A energia armazenada será:
em que . Assim sendo, utilizando a expressão para na equação acima, ficamos com:
Resposta
(a)
(b)