Capacitância equivalente
Produzido por Bruno SoaresTeoria
Fala aí, você chegou no Responde Aí! E agora vamos falar sobre Capacitância Equivalente
Então, se quiser aprender tudo se liga aqui na nossa videoaula:
Capacitância equivalente e associação de capacitores
Uma associação de capacitores ocorre quando temos dois ou mais capacitores conectados em um circuito. Em situações assim, é sempre possível substituir essa associação por um único capacitor que tenha uma capacitância equivalente.
Existem duas formas de associação de capacitores:
- Associação em série
- Associação em paralelo
Capacitores em série
Vamos começar deduzindo a fórmula da capacitância equivalente para capacitores em série. Quando temos capacitores associados em série, eles ficam assim:
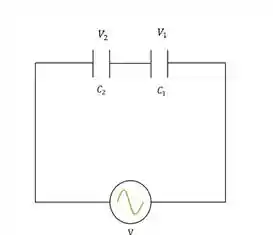
Nós vamos transformar esse circuito de cima, num circuito de capacitância equivalente mostrado na figura abaixo, se liga:
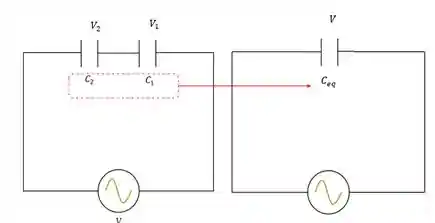
Duas coisas são importantes:
- Capacitores em série estão submetidos a voltagens diferentes.
- Os dois capacitores em série sempre armazenam cargas iguais.
Usando esses conceitos, nós temos que a capacitância de cada um é:
Podemos manipular um pouco e isolar a voltagem:
Além disso, a voltagem em dois elementos de circuito em série é a soma das voltagens:
Lembrando, que a carga nos capacitores são iguais. Então, podemos fazer isso:
E se liga a capacitância equivalente de um sistema é justamente a razão da carga total pela voltagem total do sistema
Sendo assim de modo geral temos:
E isso pode ser estendido para qualquer quantidade de capacitores:
Capacitores em Paralelo
Para deduzir a fórmula de capacitância equivalente em capacitores paralelos vamos seguir um raciocínio semelhante.
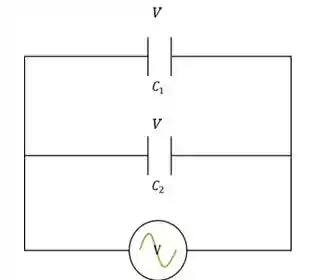
Vamos transformar o circuito de cima nesse circuito aqui, se liga:
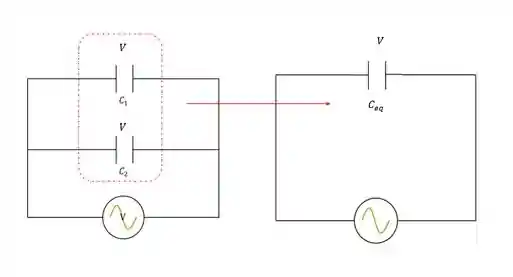
Individualmente, cada capacitor têm a seguinte capacitância:
No caso dos capacitores em paralelo temos duas regras:
- Os capacitores estarão submetidos à mesma voltagem.
- Os capacitores podem armazenar cargas diferentes.
Então a gente tem:
Aplicando os valores individuais de
Logo:
E a gente pode expandir isso pra um valor qualquer de capacitores:
Capacitores com mais de um Dielétrico
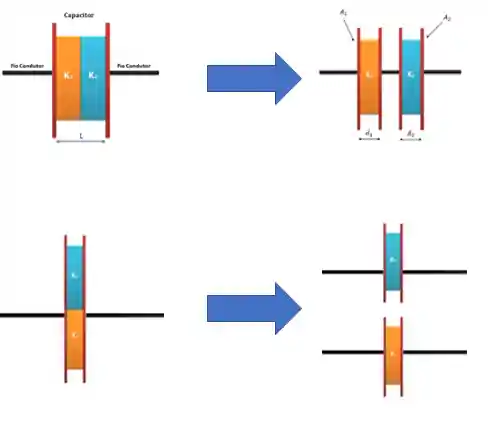
Um tipo clássico de questão é de capacitores com mais de um dielétrico. Mas não tem grilo, quando temos um capacitor assim, basta você separar cada dielétrico como se fosse um capacitor em série ou em paralelo
Videoaula de exercícios
Pra fixar bem, nada melhor que um exercício! Então confere um nessa videoaula
E é isso! Confere aqui em baixo mais exercícios de fixação 👇
Capacitores em Paralelo
Capacitores com mais de um Dielétrico
Videoaula de exercícios
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Dado o circuito abaixo:
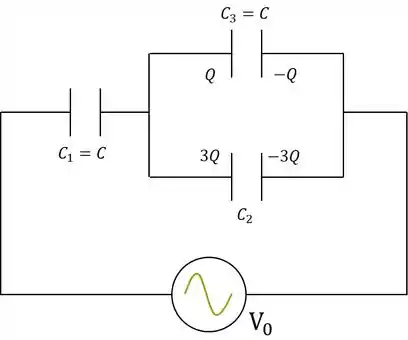
- Calcule a capacitância de em função da capacitância ;
- Calcule a capacitância equivalente do circuito todo em função da capacitância ;
Passo 1
Partiu então. Temos que na parte do circuito em que existem e paralelos, a carga em é três vezes maior que em :
Mas, ao mesmo tempo, eles estão em paralelo e portanto estão submetidos à mesma voltagem (não é a mesma que ). Dessa forma:
Dividindo ambas equações:
Substituindo o valor de :
Passo 2
Aplicando a fórmula de capacitores em paralelo:
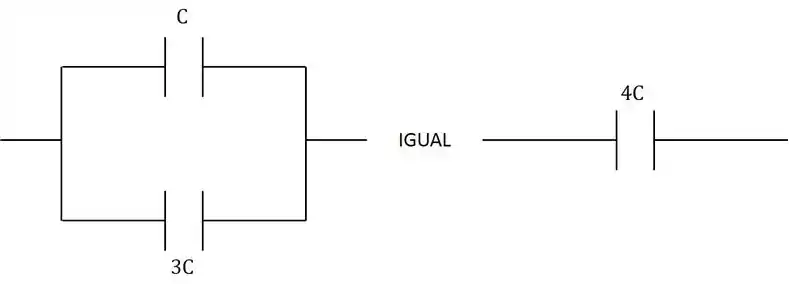
Ou seja, o circuito vira:
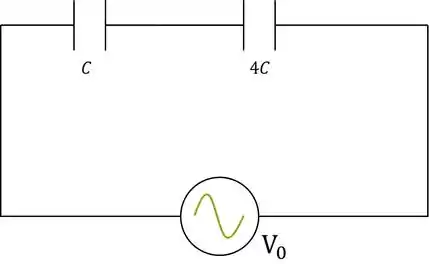
Aplicando agora a fórmula de capacitores em série:
Resposta
a)
b)
Exercício Resolvido #2
UERJ-Física III - Lista de Exercícios de Capacitores.
A figura mostra um capacitor de placas paralelas com uma área das placas e uma distância entre as placas .
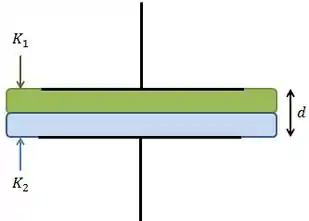
A metade superior do espaço entre as placas é preenchida por um material de constante dielétrica .
A metade inferior é preenchida por um material de constante dielétrica .
Qual é a capacitância?
Passo 1
Se observarmos bem, se uma corrente estivesse vindo de cima para baixo, por exemplo, ela passaria pelo dielétrico e depois pelo dielétrico , conseguiu visualizar?
Dá pra imaginar então que, ao invés desse troço complicado, nós poderíamos substituir isso por dois capacitores em série, um com o dielétrico e o outro com o dielétrico .
Uma forma diferente de resolver esse problema da forma apresentada na teoria é fazendo a soma das voltagens.
A voltagem resultante seria:
Sendo que, cada um desses “novos capacitores” teriam as placas separadas por .
Passo 2
A voltagem em cada um desses dielétricos é dada por:
Onde:
Sendo assim:
Agora é só jogar essa bagaça na equação que escrevemos no Passo 1.
Passo 3
Por último, vale lembrar que:
Arrumando isso aqui...
Agora sim! Só temos que fazer as contas.
Passo 4
Onde:
;
;
;
;
;
Logo:
Resposta
Exercício Resolvido #3
UFRJ-P1-2011.1-Múltipla Escolha n°3.
Um capacitor de placas planas e paralelas, de área , a distância , é “recheado” por uma chapa condutora, também de área , e espessura .

A capacitância de tal capacitor é:
Passo 1
As fórmulas que precisamos para resolver o problema são:
- Capacitância de um capacitor de placas planas paralelas de área e distância entre as placas;
- Capacitância de associação em série de dois capacitores;
- Capacitância de associação em paralelo de dois capacitores;
Passo 2
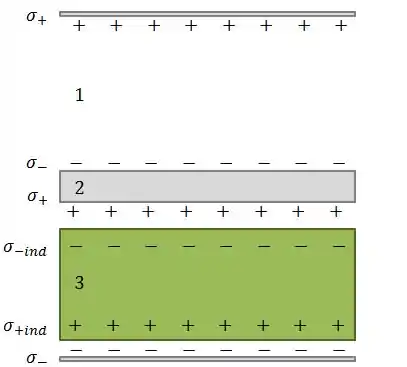
Agora, para entender o que acontece com a capacitância precisamos entender que tipo de capacitor novo nós temos. A ideia de capacitor é você conseguir separar cargas opostas por um certo espaço. Como antes nós tínhamos a seguinte configuração:
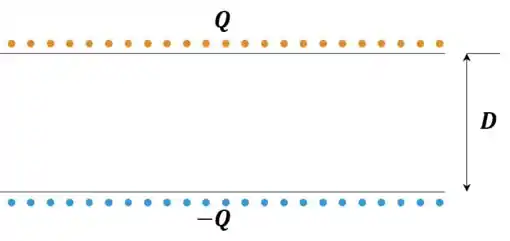
Quando inserimos uma placa condutora nesse meio, as cargas que já haviam lá (i.e. e ) vão induzir cargas na placa: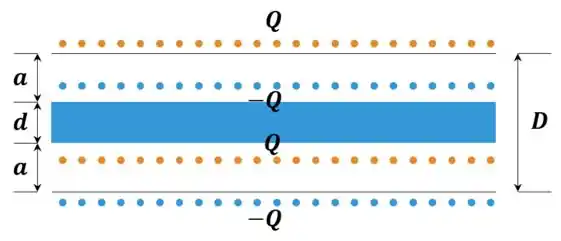
Passo 3
Portanto podemos perceber que temos dois capacitores. Agora, em série ou paralelo? Para algumas pessoas isso não é óbvio então vamos de volta ao nosso macete:
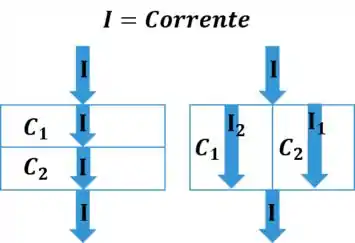
Ou seja, se a corrente “se dividir” em dois caminhos nós temos um caso de capacitores em paralelo. Se ela segue um caminho só temos série. No nosso caso temos então uma associação em série de capacitores.
Passo 4
Além disso os dois tem a mesma distância entre as placas e a mesma área, portanto:
Substituindo a fórmula de capacitores de placas planas paralelas:
Resposta
Letra c
Exercício Resolvido #4
USP-P1-2015- Questão 4
Três placas condutoras de área são espaçadas de por vácuo (região ) e de por um material de constante dielétrica (região ), como indicado na figura. A carga total na placa superior é igual a , na placa do meio é igual a zero e na placa inferior é igual a . Desconsidere a não uniformidade do campo elétrico perto das bordas.
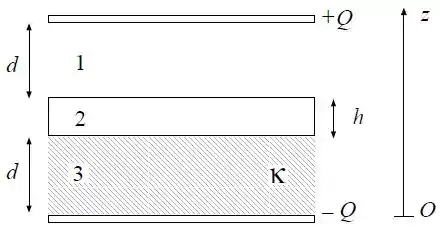
Indique numa figura e calcule as densidades de carga nas superfícies das placas condutoras. Calcule o vetor campo elétrico nas regiões e . Expresse suas respostas em termos de e.
Calcule a capacitância do sistema de três placas.
Calcule a densidade de carga de polarização no dielétrico.
Passo 1
Indique numa figura e calcule as densidades de carga nas superfícies das placas condutoras. Calcule o vetor campo elétrico nas regiões e . Expresse suas respostas em termos de e.
A densidade de carga na placa superior será:
Na placa inferior, que possui carga , a densidade de carga será:
Como as placas são condutoras, para que a placa do meio possua carga neutra, por causa da indução das cargas nas placas superior e inferior, haverá um acúmulo de carga negativa na superfície superior da placa do meio e um acúmulo de cargas positivas na superfície inferior da placa do meio.
Assim, a superfície superior da placa do meio terá densidade de carga e a superfície inferior da placa do meio terá densidade de carga .
No final das contas, o capacitor vai ter essa cara:
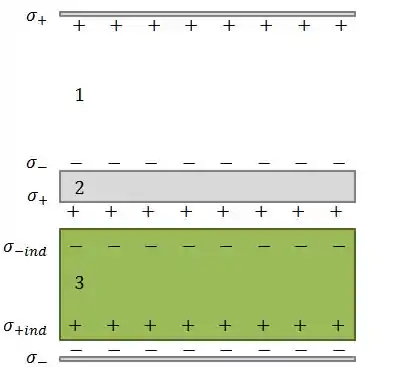
Como o problema pediu apenas a densidade de carga nas placas, não levamos em consideração a densidade de cargas induzidas que aparecerão no material dielétrico.
Passo 2
Agora temos que determinar o campo elétrico em cada uma das regiões.
- Região 1
- Região 2
- Região 3
O campo elétrico resultante está na direção vertical. Como há o acúmulo de cargas positivas na placa superior e negativas na superfície superior da placa do meio, o campo elétrico tem sentido de cima para baixo, logo:
Essa região corresponde ao interior do condutor, e aqui vai algo pra você guardar pra você no coração: O campo elétrico no interior de um condutor é sempre nulo.
Logo:
A única diferença desta para a região 1 é que, agora com o dielétrico, haverá uma variação do campo elétrico, que passará a ser dado por:
Essa mudança ocorre pois, em uma material dielétrico .
Passo 3
Calcule a capacitância do sistema de três placas.
Eu sei que pode parecer bizarro olhando assim, mas nós podemos dar uma simplificada nisso.
Ao invés de olhar para o capacitor como um sistema de três placas, podemos olhar pra isso como dois capacitores em série... o primeiro sem dielétrico e o segundo com o dielétrico.
Assim, a capacitância do sistema pode ser dada por:
Vamos chamar de a capacitância da parte sem o dielétrico. Como se tratam de placas planas e paralelas, dada por:
E de a capacitância da parte com o dielétrico:
Substituindo na fórmula da capacitância:
Passo 4
Calcule a densidade de carga de polarização no dielétrico.
O que ele tá chamando de carga de polarização aqui é o que nós chamamos de carga induzida lá no Passo 1.
No passo 2, escrevemos o campo elétrico na região 3 como:
Esse campo elétrico será a diferença entre o campo elétrico gerado pela densidade de carga (que estará de cima para baixo) e a densidade de carga (que está de baixo para cima). Logo:
Igualando as duas equações:
Todo mundo aqui está sendo dividido por , então podemos simplificar isso aqui:
Agora é só organizar isso:
Resposta
Exercício Resolvido #5
Young & Freedman, Física III Eletromagnetismo, 14ª ed. Pearson, Cap. 24, pp.138
Para o sistema de capacitores mostrado na figura abaixo, encontre a capacitância equivalente
(a) entre e ; e
(b) entre e .
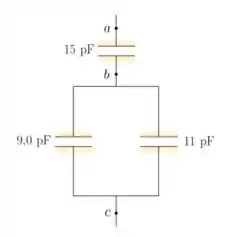
Passo 1
(a) Encontre a capacitância equivalente entre e .
Entre os terminais e , temos dois capacitores em paralelo, certo? Nesse caso, então, a capacitância equivalente é dada por:
Passo 2
(b) Encontre a capacitância equivalente entre e .
Aqui podemos pensar que temos dois capacitores em série: o capacitor de entre os terminais e e um capacitor entre os terminais e , com capacitância calculada no item (a).
Se estão em série, a capacitância equivalente será dada por:
Resposta
(a)
(b)
Exercício Resolvido #6
Sears & Zemansky, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12˚ ed., São Paulo: Addison Wesley, 2009, Problema 24.59, pp. 131.
Na Figura abaixo, e . A diferença de potencial aplicada é .
- Qual é a capacitância equivalente do circuito entre os pontos e ?
- Calcule a carga de cada capacitor e a diferença de potencial através de cada capacitor.
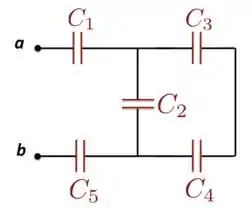
Passo 1
a) Vamos encontrar a resistência equivalente entre os capacitores e , que estão em série. Temos, então,
em que usamos o fato de que . Como está em paralelo com , a capacitância equivalente entre eles será:
em que usamos o fato de que . Dos valores dados no enunciado, a gente nota que podemos utilizar que e podemos simplificar para
Agora, está sem série com e , que são iguais. Portanto, teremos o seguinte:
em que, se utilizamos que , dá para gente que
Colocando os valores dados no enunciado, chegamos que capacitância equivalente entre os pontos e da Figura tem o seguinte valor
Passo 2
b) Para obtermos o valor da carga em cada capacitor, precisamos primeiro saber qual é a carga total do capacitor equivalente. Então
A carga dos capacitores , e , são iguais, já que eles estão em série. Tranquilo? Por isso, temos o seguinte
Agora, a diferença de potencial entre esses capacitores é diferente e, quando somadas, devem resultar em . Portanto,
Passo 3
b) Continuação...
Como e , podemos obter
Agora, essa é a diferença de potencial entre os terminais do capacitor . Por isso, a carga é
Por outro lado, e também temos a mesma diferença de potencial . Por isso, temos o seguinte
Portanto, como e estão em série, eles possuem a mesma carga
Resumindo, temos as seguintes cargas para cada um dos capacitors:
Resposta
Exercício Resolvido #7
Sears & Zemansky, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12˚ ed., São Paulo: Addison Wesley, 2009, Problema 24.72, pp. 132.
Um capacitor com placas paralelas possui o espaço entre as placas preenchido com duas camadas de dielétricos, uma com constante dielétrica e a outra com a constante dielétrica , como mostra a Figura abaixo. Cada camada possui espessura igual à distância entre as placas e cada camada preenche o espaço entre as placas. Se as placas são mantidas à uma diferença de potencial fixa , então mostre que capacitância é dada por
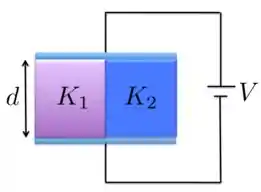
Passo 1
Neste caso, como as placas do capacitor são mantidas a uma diferença de potencial fixa , isso significa que podemos tratar o capacitor como se fosse uma associação em paralelo de dois capacitores, um com capacitância e dielétrico e outro com dielétrico , ambos com área de superfície das placas igual a e separadas por .
Por isso, temos o seguinte:
Agora, como a capacitância aumenta de um fator constante quando o capacitor é preenchido com um dielétrico e a área de cada um desses “capacitores” é , teremos
Resposta
Exercício Resolvido #8
UFRJ- Física 3 – P1 2017.1 - DIURNO - 7
Um capacitor é formado por duas placas condutoras planas e paralelas de área cada uma, separadas por uma distância muito menor que as suas dimensões. Um material isolante de constante dielétrica é inserido no capacitor de forma a ocupar metade do volume entre as placas, como mostrado na figura abaixo, ficando completamente em contato com uma delas, enquanto a outra metade permanece no vácuo. A seguir, uma diferença de potencial é aplicada entre as placas. Em termos de e , determine para esse sistema:
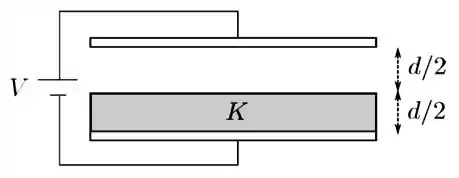
- A capacitância do sistema.
- Os módulos do campo elétrico na metade vazia () e na metade com dielétrico ().
Passo 1
- No caso particular desta questão, podemos analisar sua capacitância como se fosse resultado de uma associação em série de dois capacitores, um com capacitância , com vácuo entre suas placas, e outro com capacitância , no qual há um dielétrico com constante dielétrica , como indicado na figura abaixo.
- Para calcularmos como é o campo em cada região, precisamos da carga total armazenada no capacitor . Neste caso, a carga total é
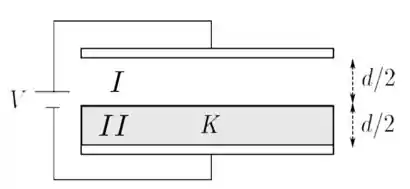
Portanto, essa capacitância resultante neste caso é
Como o capacitor está no vácuo (espaço vazio entre suas placas), sua capacitância é dada por
O capacitor , por sua vez, possui um dielétrico com constante dielétrica e tem capacitância dada por
Substituindo essas expressões em , temos
Passo 2
Na região do capacitor, “que tem o vácuo” (região vazia entre as placas), o campo elétrico , após substituir a densidade de carga acima, é
Na região do capacitor, o campo elétrico é menor que por um fator , isto é,
o que resulta em
Resposta
a)
b) ;